Описание экспериментальной установки

Баллистический маятник представляет собой массивный цилиндр M, заполненный пластилином. В цилиндр в горизонтальном направлении производят выстрел пулей массы из пружинного пистолета , неподвижно закрепленного вблизи маятника (рис. 3.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное горизонтальное отклонение маятника от его положения равновесия фиксируется механизмом .

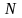Рис.3.1

Методика эксперимента и вывод рабочих формул

Энергия является универсальной количественной мерой движения и взаимодействия всех видов материи. С различными формами движения материи связывают различные виды энергии: механическую, тепловую, электромагнитную, ядерную и др.

В одних процессах форма движения материи и, соответственно, форма энергии не меняются (например, от горячего тела тепло передается холодному), в других – одна форма движения (соответственно, форма энергии) переходит в другую (например, механическая энергия в результате трения превращается в тепловую). Однако во всех случаях энергия, отданная (в той или иной форме) одним телом другому, равна энергии, полученной последним телом. В этом смысл закона сохранения энергии.

Количественно процесс обмена энергией между взаимодействующими телами в механике характеризуется работой.

Если материальное тело движется под действием силы, то работа вычисляется как

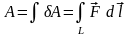, (3.1)

где 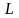– путь, пройденный телом.

Скалярная величина 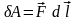называется элементарной работой силы на перемещении .

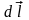Механическая энергия бывает двух видов – кинетическая и потенциальная.

Кинетическая энергия тела – мера его механического движения. Она определяется работой, которую необходимо совершить, чтобы вызвать данное движение:

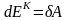. (3.2)

Для тела массой , двигающегося поступательно со скоростью , кинетическая энергия равна

. (3.3)

Потенциальная энергия – часть общей механической энергии системы тел, определяемая взаимным расположением тел и характером взаимодействия между ними.

Потенциальная энергия вводится, когда взаимодействие тел осуществляется посредством силовых полей (поле упругих сил, гравитационное поле, электрическое поле и т.д.), характеризующихся тем, что работа, совершаемая действующими в них силами при перемещении центра масс тела из одной точки в другую, не зависит от того, по какой траектории это перемещение произошло, а определяется только начальным и конечным положением тела. Такие поля называются потенциальными, а силы, действующие в них, – консервативными.

Если работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, такая сила называется неконсервативной. К числу неконсервативных сил относятся, в частности, диссипативные силы, например, силы трения и сопротивления среды.

Работа консервативных сил, действующих на тело, таким образом, равна приращению потенциальной энергии тела, взятому с противоположным знаком:

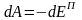, (3.4)

т.е. консервативные силы совершают работу, приводящую к убыли^ потенциальной энергии тела.

Конкретный вид функции зависит от характера силового поля. Например, потенциальная энергия тела массой , поднятого на высоту 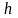над поверхностью Земли, записывается как

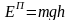. (3.5)

Выражение (3.5) свидетельствует о том, что потенциальная энергия равна работе силы тяжести при падении тела с высоты на поверхность Земли, где полагаем .

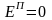Так как начало отсчета потенциальной энергии выбирается произвольно, потенциальная энергия может иметь как положительное, так и отрицательное значения (кинетическая энергия всегда положительна).

Потенциальная энергия упругодеформированного тела, например, пружины определяется формулой:

, (3.6)

где – коэффициент упругости (для пружины – жесткость); – величина деформации.

Формула (3.6) получена в предположении, что потенциальная энергия недеформированного тела равна нулю.

Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними называются силы, действующие на данное тело со стороны других тел, входящих в систему; внешними – силы, действующие со стороны тел, не входящих в данную систему.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой.

Замкнутыми системы тел могут быть только приближенно, когда можно пренебречь какими-то слабыми внешними взаимодействиями по сравнению с сильными внутренними. Например, Луна вращается вокруг Земли. Если пренебречь их взаимодействием с Солнцем и другими планетами, то можно приближенно считать данную систему замкнутой.

Для замкнутых систем существуют такие функции координат и скоростей тел (материальных точек), образующих систему, которые сохраняют при движении постоянные значения. Эти функции называются интегралами движения.

Аддитивных интегралов движения три: импульс, энергия, момент импульса. Таким образом, для замкнутых систем неизменными являются три перечисленные физические величины. В соответствии с этим имеют место три закона сохранения – законы сохранения импульса, энергии и момента импульса. Рассмотрим первые два из них.

Закон сохранения импульса. При отсутствии внешних сил (рассматриваем замкнутую систему) из второго закона Ньютона в импульсной форме для системы тел (см. (2.2)) следует

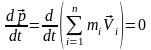, т.е. 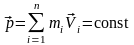, (3.7)

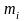где и - масса и скорость -го тела системы; 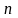- количество тел в системе.

Последнее выражение и является законом сохранения импульса: импульс замкнутой механической системы остается постоянным во времени.

Закон сохранения полной механической энергии − результат обобщения многих экспериментальных фактов. Идея закона принадлежит Ломоносову, а количественная формулировка закона дана немецкими учеными Майером и Гельмгольцем.

Итак, в замкнутой системе тел, в которой действуют только консервативные силы, полная механическая энергия системы сохраняется во времени

. (3.8)

Такие системы называются замкнутыми консервативными. Внутри системы могут происходить превращения кинетической энергии в потенциальную и обратно, но полная (суммарная) механическая энергия остается неизменной.

Для более полной и детальной информации следует обратиться к литературе, например [1-4].