
- •Р.В. Бударагин, а.В. Назаров механика. Молекулярная физика и термодинамика.
- •Оглавление
- •Введение
- •Движение тела в поле силы тяжести Лабораторная работа 1
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •Определение коэффициента трения скольжениЯ Лабораторная работа 2
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •Измерение скорости полета пули с помощью баллистического маятника Лабораторная работа 3
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод формулы, определяющей зависимость скорости полета пули от ее массы
- •2. Вывод рабочей формулы для определения скорости полета пули
- •3. Вывод формулы для определения погрешности
- •Задание к работе
- •Контрольные вопросы
- •4. Изучение абсолютно неупругого и абсолютно упругого удара Лабораторная работа 4
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод рабочей формулы для определения максимального угла отклонения подвесов шаров после абсолютно неупругого удара
- •2. Вывод рабочей формулы для определения максимальных углов отклонения подвесов шаров после абсолютно упругого удара
- •Задание к работе
- •Контрольные вопросы
- •5. Механический удар Лабораторная работа 5
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод формул для косвенных измерений скорости шарика до и после удара, силы удара и коэффициента восстановления
- •Задание к работе
- •Контрольные вопросы
- •6. Изучение основного закона динамики вращательного движения твердого тела Лабораторная работа 6
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •7. Определение момента тормозящей силы при вращательном движении и момента инерции тела
- •Лабораторная работа 7
- •Цель работы – изучение метода измерения момента тормозящей силы, действующий на тело в процессе вращения; экспериментальное определение момента инерции тела.
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •2. Вывод формулы для косвенных измерений момента инерции тела (с учетом момента тормозящей силы)
- •3. Вывод формул для расчета погрешностей косвенных измерений момента тормозящей силы и момента инерции тела
- •Задание к работе
- •Контрольные вопросы
- •8. Определение момента инерции маятника обербека Лабораторная работа 8
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Определение момента инерции маятника Обербека и момента сил сопротивления
- •2. Исследование зависимости момента инерции маятника Обербека от расстояния грузов массой , закреплённых на его стержнях, до оси вращения
- •Задание к работе
- •Контрольные вопросы
- •9. Определение момента инерции тела
- •Методом колебаний
- •Лабораторная работа 9
- •Цель работы – определение момента инерции физического маятника с применением уравнения колебаний.
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •10. Определение показателя адиабаты методом клемана и дезорма Лабораторная работа 10
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •11. Изучение фазовых превращений первого рода на примере нагревания и плавления олова Лабораторная работа 11
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •12. Обработка результатов измерений физических величин
- •Погрешности измерений физических величин
- •Обработка и представление результатов многократных измерений
- •Статистическая обработка результатов прямых измерений
- •Статическая обработка результатов косвенных измерений
- •Оформление результатов измерений
- •Цель работы.
- •Краткая теоретическая часть.
- •Экспериментальная установка и таблица измерительных приборов.
- •Расчёт измеряемых величин и их погрешностей.
- •Результаты измерений.
- •Список литературы
Движение тела в поле силы тяжести Лабораторная работа 1
Цель работы – изучение движения тела, брошенного под углом к горизонту; экспериментальная проверка теоретического выражения для дальности полета тела.
Описание экспериментальной установки
Экспериментальная
установка представляет собой пружинный
пистолет, закрепленный на высоте
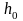 над узкой доской вблизи ее конца. Угол
наклона ствола пистолета
может изменяться. В наборе имеется
несколько пуль с различной массой m.
Поверхность доски и передняя часть пули
покрыты лентой-липой, что позволяет
предотвратить отскок пули при падении,
а также зафиксировать положение пули
для измерения дальности ее полета. Эти
измерения проводятся с помощью
закрепленной вдоль доски линейки.
над узкой доской вблизи ее конца. Угол
наклона ствола пистолета
может изменяться. В наборе имеется
несколько пуль с различной массой m.
Поверхность доски и передняя часть пули
покрыты лентой-липой, что позволяет
предотвратить отскок пули при падении,
а также зафиксировать положение пули
для измерения дальности ее полета. Эти
измерения проводятся с помощью
закрепленной вдоль доски линейки.
Методика эксперимента и вывод рабочих формул
Кинематика – раздел механики, изучающий движение тел независимо от причин, обусловливающих это движение. Во многих случаях кинематика имеет дело с материальной точкой – телом, размерами которого в условиях данной задачи можно пренебречь.
Положение
материальной
точки в
пространстве определяется заданием
трех ее координат, например, трех
декартовых координат
 ,
,
 и
и
 .
Совокупность трех величин
x,
y
и z
образует радиус-вектор,
направленный из начала координат в
точку, где находится частица (рис.1.1).
Модуль этого вектора равен:
.
Совокупность трех величин
x,
y
и z
образует радиус-вектор,
направленный из начала координат в
точку, где находится частица (рис.1.1).
Модуль этого вектора равен:
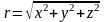 .
(1.1)
.
(1.1)

Рис.1.1
Если
точка движется, то ее положение
относительно системы отсчета меняется
со временем:
 .
Геометрическое место точек концов
радиуса-вектора представляет собой
траекторию
движения
материальной точки. Для характеристики
движения материальной точки вводится
понятие скорости.
.
Геометрическое место точек концов
радиуса-вектора представляет собой
траекторию
движения
материальной точки. Для характеристики
движения материальной точки вводится
понятие скорости.
Скорость – это векторная физическая величина, характеризующая направление и быстроту движения материальной точки:
 .
(1.2)
.
(1.2)
Скорость
направлена по касательной к траектории
движения и имеет размерность
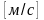 .
.
Если при движении материальной точки ее скорость меняется, то для описания этого изменения вводится понятие ускорения.
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости, как по величине, так и по направлению:
 .
(1.3)
.
(1.3)
Как
следует из (1.3) ускорение измеряется в
 .
.
Наиболее простой вид движения – это прямолинейное движение материальной точки.
Движение, при котором материальная точка за любые равные промежутки времени совершает равные перемещения, называется равномерным прямолинейным движением. Для данного типа движения справедливо:
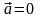 ,
,
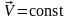 ,
(1.4)
,
(1.4)
 .
.
Движение, при котором скорость материальной точки за любые равные промежутки времени изменяется на одинаковую величину, называется равнопеременным прямолинейным движением. Для данного типа движения справедливо:
 ,
,
 ,
(1.5)
,
(1.5)
 .
.
Если
 ,
то движение называют равноускоренным,
в противном случае, когда
,
то движение называют равноускоренным,
в противном случае, когда
 ,
– равнозамедленным.
,
– равнозамедленным.
Вектор
ускорения
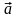 при криволинейном движении тела часто
представляют в виде суммы двух составляющих
(рис.1.2):
при криволинейном движении тела часто
представляют в виде суммы двух составляющих
(рис.1.2):
 ,
(1.6)
,
(1.6)
где
 − тангенциальное ускорение, направленное
по касательной к траектории движения;
− тангенциальное ускорение, направленное
по касательной к траектории движения;
 −
нормальное ускорение, направленное по
нормали к траектории (перпендикулярно
касательной) к центру её кривизны.
−
нормальное ускорение, направленное по
нормали к траектории (перпендикулярно
касательной) к центру её кривизны.

Рис.1.2
Из рисунка видно, что модуль полного ускорения равен
 .
(1.7)
.
(1.7)
Тангенциальное ускорение характеризует быстроту изменения скорости по величине, следовательно,
 .
(1.8)
.
(1.8)
Нормальное ускорение определяет быстроту изменения скорости по направлению и численно определяется как
 ,
(1.9)
,
(1.9)
где R − радиус кривизны траектории в данной точке.
Для более полной и детальной информации следует обратиться к литературе, например [1-4].
Тело
(пуля), брошенное под углом
к горизонту (рис.1.3), движется под действием
силы тяжести. Если другими силами
(например, сопротивлением воздуха) можно
пренебречь, то движение называют
свободным
падением.
Ускорение при этом называют ускорением
свободного падения
 .
Оно направлено вертикально вниз и в
условиях опыта может считаться постоянным
по модулю.
.
Оно направлено вертикально вниз и в
условиях опыта может считаться постоянным
по модулю.

Рис.1.3
Движение тела можно описать следующими векторными кинематическими уравнениями:
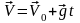 ,
(1.10)
,
(1.10)
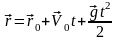 ,
(1.11)
,
(1.11)
где
 – вектор скорости пули в момент времени
– вектор скорости пули в момент времени
 ;
;
 – вектор скорости пули при
– вектор скорости пули при
 (начальная скорость);
(начальная скорость);
 –
радиус-вектор, определяющий местоположение
пули в момент времени t
относительно начала координат;
–
радиус-вектор, определяющий местоположение
пули в момент времени t
относительно начала координат;
 – радиус-вектор в момент времени
.
– радиус-вектор в момент времени
.
В проекциях на ось X, направленную горизонтально в сторону полета пули, и ось Y, направленную вертикально вверх (рис.1.3), уравнения (1.10) и (1.11) имеют вид:
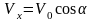 ;
(1.12)
;
(1.12)
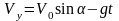 ;
(1.13)
;
(1.13)
 ;
(1.14)
;
(1.14)
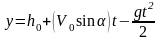 .
(1.15)
.
(1.15)
Таким
образом, это сложное движение материальной
точки (пули) можно рассматривать как
результат сложения двух движений:
равномерного
прямолинейного движения по оси
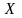 и равнопеременного прямолинейного
движения по оси
и равнопеременного прямолинейного
движения по оси
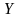 .
.
Скорость
пули сразу после выстрела можно
определить, стреляя первоначально в
горизонтальном направлении ( ).
Из (1.14) и (1.15) при этом получим:
).
Из (1.14) и (1.15) при этом получим:
 .
(1.16)
.
(1.16)
где
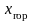 – дальность полета пули.
– дальность полета пули.
Таким
образом, произведя выстрел в горизонтальном
направлении с высоты
,
и измерив дальность полета пули
,
по формуле (1.16) можно вычислить ее
начальную скорость
 .
Эта скорость определяется потенциальной
энергией сжатой пружины пистолета, она
практически не зависит от угла .
.
Эта скорость определяется потенциальной
энергией сжатой пружины пистолета, она
практически не зависит от угла .
Теперь
рассмотрим полет пули, пущенной под
углом
к горизонту с высоты
.
В точке падения координата
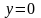 .
Используя (1.14) и (1.15), обозначив дальность
полета пули
.
Используя (1.14) и (1.15), обозначив дальность
полета пули
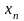 ,
получим формулу для расчета этой
величины:
,
получим формулу для расчета этой
величины:
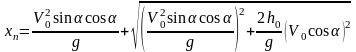 ,
(1.17)
,
(1.17)
где определяется по формуле (1.16).
