2. Вывод формулы для косвенных измерений момента инерции тела (с учетом момента тормозящей силы)

Рассмотрим систему «тело-груз» в начальный момент времени, когда груз находится на отметке , а в качестве конечного выберем тот момент времени, когда груз опустился до нижней отметки , соответствующей полной длине нити. Опять будем исходить из энергетического соотношения (7.1).

Для выбранных начального и конечного состояний получим

, (7.7)

где 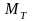– момент тормозящей силы (7.6); – угол поворота тела, соответствующий перемещению груза от отметки до и определяемый по формуле (7.4).

Начальная механическая энергия системы «тело-груз» равна

. (7.8)

Конечная механическая энергия системы складывается из кинетической энергии вращательного движения тела и кинетической энергии поступательного движения груза в момент прохождения им отметки :

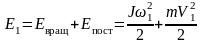, (7.9)

где – момент инерции тела; 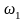– угловая скорость вращения тела в момент (рис.7.1); – скорость поступательного движения груза в момент .

Таким образом, в процессе движения груз за счет упругого растяжения нити опускается чуть ниже отметки , тормозится нитью, а затем за счет упругого сжатия нити возвращается на эту отметку.

Предполагая, что движение системы является равноускоренным, для скорости груза на отметке получаем

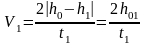, (7.10)

где – время, за которое груз опустится от отметки до .

Угловая скорость вращения тела в тот же момент времени равна

, (7.11)

где – радиус шкива, на который намотана нить.

Подставляя (7.7), (7.8), (7.9) в (7.1), получим

.

Из этой формулы, учитывая (7.4), (7.10) и (7.11), выражаем момент инерции :

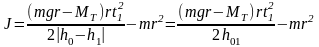, (7.12)

где – момент тормозящей силы, который вычисляется по формуле (7.6).

3. Вывод формул для расчета погрешностей косвенных измерений момента тормозящей силы и момента инерции тела

Методика определения оценок истинных значений величин и погрешностей при прямых и косвенных измерениях описана в главе «Обработка результатов измерений физических величин». При выполнении данной лабораторной работы прямыми будут являться измерения длины 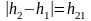и времени . Остальные величины, входящие в рабочие формулы (7.6) и (7.12), измеряются заранее и их истинные значения с указанием погрешностей приведены в таблице исходных данных, помещенной около экспериментальной установки.

Выполнив прямые многократные измерения величин и (см. задание к работе) и проведя их статистическую обработку по методике, описанной в гл.12, найдите 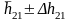и 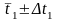для выбранного значения доверительной вероятности. Эти величины будут в дальнейшем использованы для оценки истинного значения и погрешности при косвенных измерениях.

Подставляя в рабочую формулу (7.6) истинные значения всех аргументов, получим оценку истинного значения момента тормозящей силы:

, (7.13)

где черта над величиной означает «оценка истинного значения».

Абсолютная погрешность косвенных измерений величины 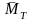определяется формулой

.

Взяв частные производные по всем аргументам, получаем

. (7.14)

В формулу (7.14) входят пять квадратичных членов. Вклад каждого из них в погрешность величины не одинаков. Поэтому, чтобы упростить вычисления, прежде чем применять эту формулу, необходимо оценить вклад каждого квадратичного слагаемого и оставить в формуле только наибольшие. Эта оценка, кроме того, позволит выявить те величины, точность измерения которых определяет точность получаемого результата.

Оценку истинного значения величины момента инерции тела, определяемого в опытах с помощью формулы (7.12), получим, подставив в нее истинные значения входящих аргументов:

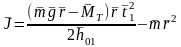. (7.15)

Абсолютная погрешность косвенных измерений величины 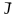определяется формулой

.

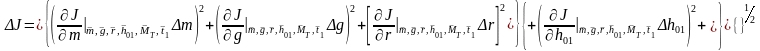Взяв частные производные по всем аргументам, получаем

. (7.16)

В формулу (7.16) входит шесть квадратичных членов. Один из них (пятый) связан с погрешностью величины , которая определяется формулой (7.14). Как было отмечено ранее, прежде, чем применять формулу (7.16), необходимо оценить вклад каждого квадратичного слагаемого, сохранив только наибольшие.