Контрольные вопросы

1. Какова цель данной лабораторной работы?

2. Покажите, что .

3. Что такое момент силы? Как определить модуль и направление момента силы?

4. Какая сила создает вращающий момент крестовины и как он определяется в данной работе? Выполнение каких условий необходимо, чтобы момент силы был постоянным?

5. Что такое угловая скорость? Как определить её направление?

6. Найдите величину и направление углового ускорения крестовины. Какими правилами при этом следует руководствоваться?

7. В чем заключается основной закон динамики вращательного движения абсолютно твердого тела? Сделайте запись в векторной форме.

8. Что такое момент инерции? От чего он зависит? Как рассчитать его для симметричных тел относительно неподвижной оси?

9. Что такое момент импульса материальной точки и тела? От чего он зависит? Как он определяется в данной работе?

10. Метод определения отношений ; ; . Какие условия необходимы, чтобы выполнялось каждое из приведенных равенств?

7. Определение момента тормозящей силы при вращательном движении и момента инерции тела

Лабораторная работа 7

Цель работы – изучение метода измерения момента тормозящей силы, действующий на тело в процессе вращения; экспериментальное определение момента инерции тела.

Описание экспериментальной установки

Установка представляет собой тело со шкивом, которое вращается в шарикоподшипниках. На шкив намотана нить, один конец которой прикреплен к шкиву, а другой – к подставке массой 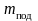. На подставку могут помещаться подгрузки массой . Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того, как груз от отметки опустится на полную длину нити до отметки 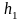(рис7.1), тело, вращаясь по инерции, поднимет груз снова на некоторую высоту до отметки h₂.

Рис.7.1

В процессе движения часть механической энергии системы «тело-груз» расходуется на работу против тормозящей силы и, следовательно, превращается во внутреннюю энергию системы и окружающего воздуха, которые нагреваются. Из этого следует, что тело поднимет груз на высоту меньшую начальной, то есть отметка всегда будет расположена ниже отметки . Тормозящая сила складывается из силы трения в подшипниках и из силы трения о воздух при движении тела и груза.

Методика эксперимента и вывод рабочих формул

1. Вывод формулы для косвенных измерений момента тормозящей силы

Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей силы при переходе системы «тело-груз» из начального состояния в конечное равна

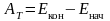, (7.1)

где – механическая энергия системы «тело-груз» в начальном состоянии; – механическая энергия системы «тело-груз» в конечном состоянии.

Механическая энергия системы складывается из кинетической и потенциальной энергий. В те моменты времени, когда система покоится, кинетическая энергия равна нулю и, следовательно, механическая энергия становится равной только потенциальной энергии системы. Такие состояния системы возникают в начальный момент времени, когда груз находится на отметке , и в тот момент, когда, спустившись вниз, груз за счет вращения тела поднимается до отметки (рис.7.1). Если принять, что на высоте потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно

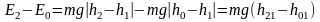, (7.2)

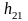где m – масса подставки с подгрузками; – расстояние между отметками и ; – расстояние между отметками и .

Будем считать, что момент тормозящей силы в основном связан с вращательным движением тела, т. е. тормозящей силой, действующей на груз, пренебрежем. Тогда элементарная работа момента тормозящей силы равна скалярному произведению

,

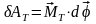где – вектор момента тормозящей силы; – вектор бесконечно малого углового перемещения тела.

Оба вектора и направлены вдоль оси вращения, но в противоположные стороны. Следовательно,

.

Полная работа тормозящей силы, если предположить, что ее момент постоянен, равна

, (7.3)

где – угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки до отметки ).

При движении груза вниз от отметки до отметки со шкива сматывается нить длиной . Учитывая, что длина окружности шкива равна 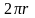и каждый оборот шкива соответствует углу радиан, найдем угол поворота шкива при движении груза вниз:

радиан. (7.4)

Очевидно, что при дальнейшем вращении тела до момента, когда груз остановится на отметке , оно повернется на угол

радиан.

Тогда общий угол поворота тела, соответствующий движению груза от отметки до отметки , равен

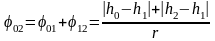радиан. (7.5)

Подставляя (7.2) и (7.3) в (7.1), найдем

.

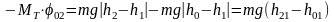Отсюда, используя (7.5), получаем формулу для определения величины момента тормозящей силы

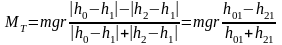. (7.6)