
- •Р.В. Бударагин, а.В. Назаров механика. Молекулярная физика и термодинамика.
- •Оглавление
- •Введение
- •Движение тела в поле силы тяжести Лабораторная работа 1
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •Определение коэффициента трения скольжениЯ Лабораторная работа 2
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •Измерение скорости полета пули с помощью баллистического маятника Лабораторная работа 3
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод формулы, определяющей зависимость скорости полета пули от ее массы
- •2. Вывод рабочей формулы для определения скорости полета пули
- •3. Вывод формулы для определения погрешности
- •Задание к работе
- •Контрольные вопросы
- •4. Изучение абсолютно неупругого и абсолютно упругого удара Лабораторная работа 4
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод рабочей формулы для определения максимального угла отклонения подвесов шаров после абсолютно неупругого удара
- •2. Вывод рабочей формулы для определения максимальных углов отклонения подвесов шаров после абсолютно упругого удара
- •Задание к работе
- •Контрольные вопросы
- •5. Механический удар Лабораторная работа 5
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Вывод формул для косвенных измерений скорости шарика до и после удара, силы удара и коэффициента восстановления
- •Задание к работе
- •Контрольные вопросы
- •6. Изучение основного закона динамики вращательного движения твердого тела Лабораторная работа 6
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •7. Определение момента тормозящей силы при вращательном движении и момента инерции тела
- •Лабораторная работа 7
- •Цель работы – изучение метода измерения момента тормозящей силы, действующий на тело в процессе вращения; экспериментальное определение момента инерции тела.
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •2. Вывод формулы для косвенных измерений момента инерции тела (с учетом момента тормозящей силы)
- •3. Вывод формул для расчета погрешностей косвенных измерений момента тормозящей силы и момента инерции тела
- •Задание к работе
- •Контрольные вопросы
- •8. Определение момента инерции маятника обербека Лабораторная работа 8
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •1. Определение момента инерции маятника Обербека и момента сил сопротивления
- •2. Исследование зависимости момента инерции маятника Обербека от расстояния грузов массой , закреплённых на его стержнях, до оси вращения
- •Задание к работе
- •Контрольные вопросы
- •9. Определение момента инерции тела
- •Методом колебаний
- •Лабораторная работа 9
- •Цель работы – определение момента инерции физического маятника с применением уравнения колебаний.
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •10. Определение показателя адиабаты методом клемана и дезорма Лабораторная работа 10
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •11. Изучение фазовых превращений первого рода на примере нагревания и плавления олова Лабораторная работа 11
- •Описание экспериментальной установки
- •Методика эксперимента и вывод рабочих формул
- •Задание к работе
- •Контрольные вопросы
- •12. Обработка результатов измерений физических величин
- •Погрешности измерений физических величин
- •Обработка и представление результатов многократных измерений
- •Статистическая обработка результатов прямых измерений
- •Статическая обработка результатов косвенных измерений
- •Оформление результатов измерений
- •Цель работы.
- •Краткая теоретическая часть.
- •Экспериментальная установка и таблица измерительных приборов.
- •Расчёт измеряемых величин и их погрешностей.
- •Результаты измерений.
- •Список литературы
2. Вывод рабочей формулы для определения максимальных углов отклонения подвесов шаров после абсолютно упругого удара
Абсолютно упругим называется удар, при котором не происходит превращение механической энергии соударяющихся тел в другие виды энергии. В частности, не наблюдается нагревание тел при ударе. При абсолютно упругом ударе деформация тел, возникающие в момент удара, после его завершения полностью исчезает. Очень близким к упругому является удар стальных шаров.
В работе рассматривается соударение двух стальных шаров массами и , закрепленных на подвесах одинаковой длины (рис. 4.1).
Найдем
скорости шаров сразу после удара, который
будем считать абсолютно упругим лобовым.
Пусть скорость шара
за мгновение до удара равна
,
а шара
– нулю. Скорости шаров сразу после удара
обозначим
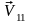 и
и
 соответственно. Как и в случае абсолютно
неупругого соударения, механическую
систему двух шаров во время абсолютно
упругого удара можно считать замкнутой
в горизонтальном направлении (вдоль
оси X).
Следовательно, для составляющей вектора
импульса механической системы,
параллельной оси X,
должен выполняться закон сохранения:
соответственно. Как и в случае абсолютно
неупругого соударения, механическую
систему двух шаров во время абсолютно
упругого удара можно считать замкнутой
в горизонтальном направлении (вдоль
оси X).
Следовательно, для составляющей вектора
импульса механической системы,
параллельной оси X,
должен выполняться закон сохранения:
 ,
(4.8)
,
(4.8)
где
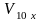 ,
,
 и
и
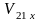 – проекции векторов
,
и
на ось X.
– проекции векторов
,
и
на ось X.
При абсолютно упругом ударе выполняется закон сохранения полной механической энергии системы соударяющихся тел. Тогда, полагая потенциальную энергию шаров в момент удара равной нулю, имеем:
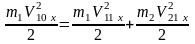 .
(4.9)
.
(4.9)
В (4.9) учли, что векторы скоростей шаров за мгновение до и сразу после удара направлены горизонтально.
Решая систему уравнений (4.8)-(4.9) относительно и , получаем:
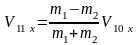 ,
(4.10)
,
(4.10)
 .
(4.11)
.
(4.11)
Анализ формул (4.10) и (4.11) показывает:
если
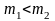 ,
то
,
то
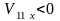 .
Это означает, что после упругого удара
шаром меньшей массы по неподвижному
шару с большей массой, меньший шар после
удара движется в обратную сторону;
.
Это означает, что после упругого удара
шаром меньшей массы по неподвижному
шару с большей массой, меньший шар после
удара движется в обратную сторону;если
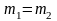 ,
то
,
то
 ,
а
,
а
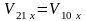 .
При равенстве масс соударяющихся шаров
в результате упругого удара первый шар
останавливается, а второй начинает
двигаться со скоростью первого шара;
.
При равенстве масс соударяющихся шаров
в результате упругого удара первый шар
останавливается, а второй начинает
двигаться со скоростью первого шара;если
 ,
то
,
то
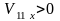 .
Это означает, что оба шара после удара
движутся в положительном направлении
оси X.
.
Это означает, что оба шара после удара
движутся в положительном направлении
оси X.
Рассмотрим интересный физический эффект, наблюдающийся при упругом повторном соударении шара массы с первоначально неподвижным шаром массы .
Будем
считать, что периоды колебаний шаров
одинаковы. Тогда после первого соударения
шары, отклонившись от первого положения
равновесия, повторно столкнуться в той
же нижней точке их траекторий. За время
одного колебания потери механической
энергии каждого шара, связанные с работой
силы сопротивления воздуха, малы. Это
позволяет считать, что их скорости за
мгновение до повторного удара равны по
модулю скоростям шаров сразу после
первого удара, но направление скоростей
противоположны, т.е.
 и
и
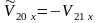 .
Тогда для повторного соударения закон
сохранения проекции вектора импульса
системы на ось X
и закон сохранения механической энергии
запишутся в виде:
.
Тогда для повторного соударения закон
сохранения проекции вектора импульса
системы на ось X
и закон сохранения механической энергии
запишутся в виде:
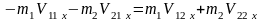 ,
(4.12)
,
(4.12)
 ,
(4.13)
,
(4.13)
где
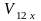 и
и
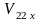 – проекции скоростей
– проекции скоростей
 и
и
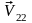 шаров сразу после второго удара на ось
X.
шаров сразу после второго удара на ось
X.
Подставляя (4.10) и (4.11) в (4.12) и (4.13), после преобразований получаем:
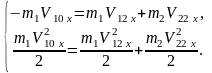
Откуда
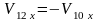 ,
,
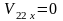 .
.
Таким образом, в результате второго удара шар , который до первого удара покоился, опять останавливается, а шар приобретает кинетическую энергию, равную энергии перед первым ударом. Последнее означает, что после второго удара шар должен отклониться почти на тот же угол, с которого он был отпущен электромагнитом в начале опыта.
Так как величинами, которые будут измеряться в опытах, являются не скорости, а максимальные углы отклонения подвесов шаров от положения равновесия, получим формулы для углов отклонения каждого из шаров после первого удара, используя полученные выражения для скоростей (4.10) и (4.11).
Пусть удерживаемый электромагнитом шар имеет подвес, расположенный под углом к вертикальному направлению. Если расстояние от оси вращения до центра масс шара равно l (рис. 4.1), то в таком положении центр масс поднят на высоту , которая равна
.
Из закона сохранения механической энергии следует
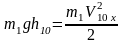 .
.
Откуда
 .
(4.14)
.
(4.14)
Из формулы (4.10), подставляя (4.14), получаем
 .
(4.15)
.
(4.15)
Угол
отклонения подвеса первого шара после
первого удара обозначим
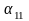 .
Связь этого угла с высотой подъема после
первого удара
.
Связь этого угла с высотой подъема после
первого удара
 имеет вид:
имеет вид:
 .
(4.16)
.
(4.16)
Опять воспользуемся законом сохранения механической энергии
 ,
,
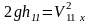 .
(4.17)
.
(4.17)
Подставляя (4.15) и (4.16) в (4.17), получаем
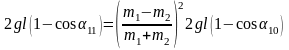 .
.
После сокращений и преобразований получим рабочую формулу для косинуса максимального угла отклонения подвеса первого шара после первого удара:
 .
(4.18)
.
(4.18)
Рассуждая
аналогично, получим рабочую формулу
для косинуса максимального угла
отклонения
 подвеса второго шара после первого
удара:
подвеса второго шара после первого
удара:
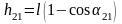 ;
;
 ;
;
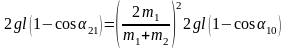 ;
;
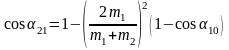 .
(4.19)
.
(4.19)
Пользуясь
рабочими формулами (4.18) и (4.19), найдем,
при каком отношении масс шаров
 максимальные углы отклонения их подвесов
после первого удара будут одинаковыми.
максимальные углы отклонения их подвесов
после первого удара будут одинаковыми.
При
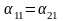 из (4.18) и (4.19) получаем:
из (4.18) и (4.19) получаем:
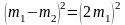 .
.
Откуда
 .
.
Таким образом, максимальные углы отклонения подвесов шаров после первого удара будут одинаковыми, если отношение массы второго шара к массе первого равно
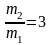 .
(4.20)
.
(4.20)
Для более полной и детальной информации следует обратиться к литературе, например [1-4].
