Построение области допустимых решений задачи

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.

5.3. Симплекс-метод решения задач лп

В общем виде схема решения задач линейного программирования (ЛП) заключается в последовательном переборе всех допустимых решений и выборе «наилучшего», т.е. оптимального решения с точки зрения целевой функции. Однако, если число допустимых решений велико, то такая задача становится труднореализуемой. Суть симплекс-метода заключается в целенаправленном переборе допустимых решений, при котором целевая функция «улучшается», или, по крайней мере, «не ухудшается» на каждом последующем шаге решения (итерации).

Рассмотрим следующую ЗЛП в канонической форме:

,

, , (5.15)

.

Любые m переменных системы ограничений ЗЛП (5.15), состоящей из m линейно независимых уравнений с n переменными (m<n), называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n–m переменных называются неосновными (или свободными).

Базисным называют решение ЗЛП, при котором все свободные переменные равны нулю. Допустимым базисным решением (опорным планом) называют базисное решение, удовлетворяющее условию неотрицательности, т.е. .

Опорный план называют невырожденным, если он содержит ровно m положительных компонент, в противном случае, он является вырожденным.

Алгоритм симплекс-метода можно представить в виде следующей схемы:

Рис. 5.7.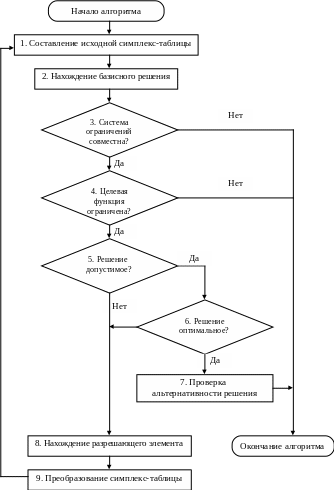 Алгоритм симплекс-метода

Таким образом, алгоритм симплекс-метода можно представить в виде следующих этапов:

1. Представление исходной задачи в виде симплекс таблицы.

Для получения исходной симплекс-таблицы общую или стандартную задачу линейного программирования необходимо привести к каноническому виду путем введения дополнительных неотрицательных переменных.

Если задача линейного программирования изначально задана в канонической форме, то необходимо выделить базисные переменные в системе ограничений, используя, к примеру, метод Жордана-Гаусса.

Пусть с помощью метода Жордана-Гаусса в системе ограничений задачи (5.15) выделили базисные переменные х₁, х₂, …, х_m:

(5.16)

где – полученные в результате элементарных преобразований значения величин a_ij и b_i соответственно (причем - не обязательно положительные);

x_m+1, x_m+2, …, x_n – свободные переменные.

Выразим в системе (5.16) базисные переменные через свободные:

(5.17)

Подставим в целевую функцию задачи линейного программирования (5.15) полученные значения базисных переменных, приведем подобные, в результате получим:

(5.18)

где - сумма величин ;

– полученные в результате преобразований значения коэффициентов при переменных x_m+1, x_m+2, …, x_n соответственно;

– не обязательно положительные.

Представим полученные систему ограничений и целевую функцию в виде следующей таблицы:

Таблица 5.1

Исходная симплекс-таблица

Свободные переменные Базисные переменные	Свободные числа,					Оценочные отношения,

Примечание: величины и в таблице приводятся со своими знаками, которые они имеют в системе ограничений (5.17) и целевой функции (5.18) без раскрытия скобок.

Данную таблицу называют симплекс-таблицей, на основе которой проводятся последующие преобразования.