4 Этап: решение скорректированной задачи.

Решая полученную задачу симплекс-методом, на последней итерации получим следующую симплекс-таблицу:

Таблица 6.28

Исходная симплекс-таблица

СП БП				Оценочные отношения
	2	-1	1
	27	0	1

Оптимальное решение , является альтернативным. Однако оптимальный план не удовлетворяет условию целочисленности исходной задачи (оптимальное значение переменной является дробным).

II итерация

1 Этап: формирование правильного отсечения.

Сформируем правильное отсечение в соответствии с формулами (6.22), (6.23) по уравнению соответствующему переменной (строке соответствующей переменной в симплекс-таблице 6.28):

.

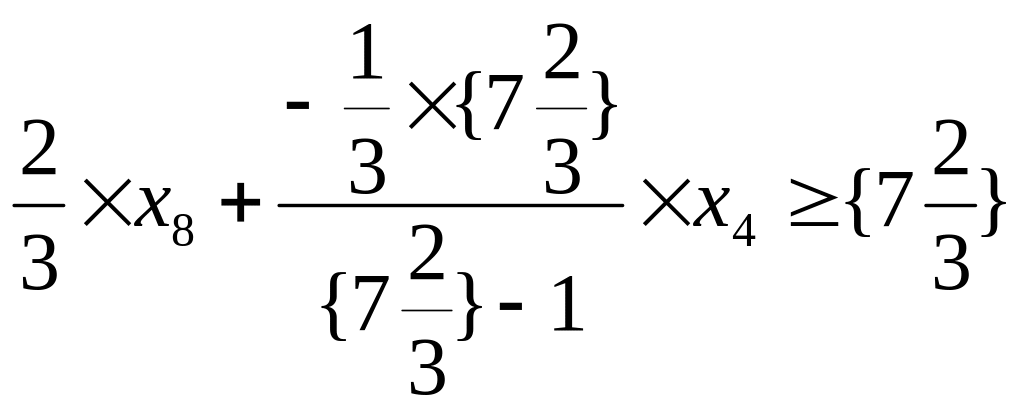
2 Этап: корректировка исходной задачи с ослабленными ограничениями с учетом правильного отсечения.

Приведем полученное неравенство к равносильному уравнению:

,

где .

Скорректируем исходную задачу с ослабленными ограничениями с учетом очередного правильного отсечения (для удобства корректировку осуществим на основе равносильной задачи, полученной в симплекс-таблице 6.28).

Примем в качестве базисной переменную и выразим ее через свободные переменные:

.

Впишем данное уравнение в симплекс-таблицу 10.28:

Таблица 6.29

Исходная симплекс-таблица

СП БП				Оценочные отношения
	2	-1	1
	27	0	1

3 Этап: решение скорректированной задачи.

Решая полученную задачу симплекс-методом, на последней итерации получим следующую симплекс-таблицу:

Таблица 6.30

Исходная симплекс-таблица

СП БП				Оценочные отношения
	16	-1
	3	2
	6	-1	1
	11	3	-2
	7	-1	1
	1	1	-1
	1	1
	27	1	0

Оптимальное решение , является альтернативным. Оптимальный план удовлетворяет условию целочисленности исходной задачи.

Ответ: – оптимальное альтернативное решение; .