Г еометрический смысл дифференциала
На
графике функции 
возьмем
произвольную точку 
и
дадим аргументу 
приращение 
.
При этом функция получит приращение 
(на
рисунке отрезок 
).
Проведем касательную
к кривой
в
то чке 
и
обозначим угол ее наклона к оси 
через 
,
тогда
.
Из треугольника 
находим 
,
т.е. 
.
Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции в данной точке, когда аргумент получает приращение .
Дифференцируемость функции. Необходимые и достаточные условия дифференцируемости.
Функция y=f(x), имеющая производную в точке x0, называется дифференцируемой в этой точке.
Функция y=f(x) называется дифференцируемой в интервале (a,b), если она дифференцируема в каждой точке этого интервала.
Необходимое условие дифференцируемости:
Если функция u = f(x1, x2, … , xn) дифференцируема в точке a , то в этой точке существуют частные производные по каждому аргументу x1, … , xn , причем
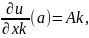
где Ak — некоторые числа, не зависящие от Δxk ( k = 1,2, … ,n )
Достаточное условие дифференцируемости
Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную.
Таблица производных и дифференциалов основных элементарных функций.
Производная и дифференциал суммы, произведения и частного
Дифференциал суммы, произведения и частного:
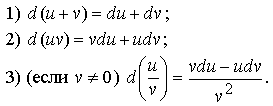
Производная суммы, произведения и частного:
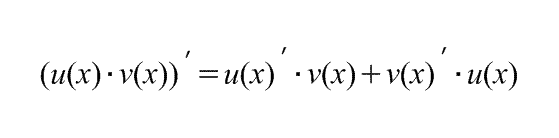
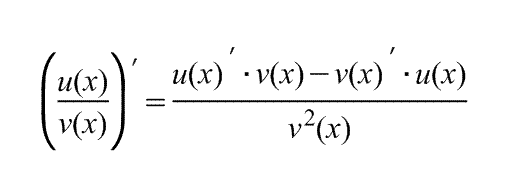
Производная сложной функции и обратной функции
Производная сложной функции
Если f и g -
дифференцируемые функции, то сложная
функция 
также
дифференцируема по x и
ее производная равна
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно иметь ввиду, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!
Можно заметить, что производная сложной функции представляется в виде последовательного произведения производных составляющих функций, причем аргументы функций согласованы (сцеплены) таким образом, что значение внутренней функции служит аргументом для следующей за ней внешней функции. Поэтому правило дифференцирования сложной функции часто называют "цепным правилом" (chain rule).
Производная обратной функции
Пусть
функция 
имеет
в точке 
производную 
.
Тогда обратная функция 
имеет
в соответствующей точке 
производную 
,
которую можно отыскать по формуле
|
Если
существует производная 
,
то разностное отношение 
стремится
к 
при 
,
что соответствует вертикальной
касательной к графику 
при 
(если
считать, что ось 
расположена
горизонтально, а ось 
--
вертикально).
Производные высших порядков
Производные высшего порядка явно заданной функции
Пусть функция y = f(x) имеет конечную производную f '(x) в некотором интервале (a, b), т.е. производная f '(x)также является функцией в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции f, которая обозначается в виде
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функцииf:
Производные более высокого порядка (если они существуют) определяются как
Таким образом, понятие производной n-го порядка вводится индуктивно путем последовательного вычисления n производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы
В ряде случаев можно вывести общую формулу для производной произвольного n-го порядка без вычисления промежуточных производных. Некоторые такие примеры рассмотрены ниже. Отметим, что для нахождения производных высшего порядка можно использовать следующие линейные соотношения:
Производные высшего порядка неявно заданной функции
Производная n-го порядка неявно заданной функции находится последовательным (n раз) дифференцированием уравнения F(x, y) = 0. На каждом шаге, после соответствующих подстановок и преобразований, можно получить явное выражение для производной, зависящее лишь от переменных x, y, т.е. производные имеют вид
Производные высшего порядка функции, заданной параметрически
Рассмотрим функцию y = f(x), заданную параметрически с помощью двух уравнений
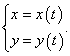
Первая производная данной функции выражается формулой
Дифференцируя еще раз по x, находим производную второго порядка:
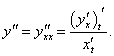
Аналогично определяются производные третьего и более высокого порядка:
