
- •Переменные и постоянные величины
- •Множества. Операции над множествами. Символика математической логики.
- •Действительные числа и их свойства
- •Понятие окрестности точки. Точки прикосновения, предельные , граничные и внутренние точки множества.
- •Открытые и замкнутые множества. Отрезок, интервал, промежуток действительной прямой. Ограниченные множества.
- •Понятие отображения (функции). Образы и прообразы множеств.
- •Способы задания функций. Обратная функция, сложная функция
- •Ограниченные и монотонные последовательности
- •Теорема о единственности предела
- •Теорема о необходимом условии сходимости числовой последовательности.
- •Свойства сходящихся последовательностей, связянные с арифметическими действиями и неравенствами
- •Предел функции
- •Бесконечно большие, бесконечно малые и эквивалентные величины, о- символика.
- •Основные виды неопределенностей
- •Замечательные пределы
- •Непрерывность функции в точке и на множестве. Арифметические операции над непрерывными функциями.
- •Свойства функция, непрерывных на отрезке
- •Основные теоремы о функциях, непрерывных на отрезке
- •Точки разрыва и их классификации
- •Производная и дифференциал функции. Связь с непрерывностью.
- •Г еометрический смысл дифференциала
- •Дифференцируемость функции. Необходимые и достаточные условия дифференцируемости.
- •Производная и дифференциал суммы, произведения и частного
- •Производная сложной функции и обратной функции
- •Производные высших порядков
- •Механическое истолкование второй производной
- •Дифференциалы высших порядков
- •Признаки постоянства, возрастания и убывания функций на промежутке
- •Нахождение максимумов и минимумов функции с помощью производных
- •Нахождение наименьшего и наибольшего значения функции на заданном промежутке
- •Правило раскрытия неопределенности Лопиталя-Бернулли
- •Касательная к плоской кривой. Выпуклость и вогнутость плоской кривой
- •Точки перегиба графика функции. И нахождение.
- •Асимптоты
- •Построение графика функции на основе её полного анализа.
- •Первообразная функция. Неопределенный интеграл и его основные свойства
- •Основные методы интегрирования
Точки разрыва и их классификации
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
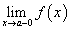 и
правосторонний предел
и
правосторонний предел 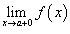 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов ![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Производная и дифференциал функции. Связь с непрерывностью.
Производная (функции
в точке) — основное понятие дифференциального
исчисления, характеризующее скорость
изменения функции (в данной точке).
Определяется как предел отношения
приращения функции к приращению ее
аргумента при
стремлении п риращения
аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке).
риращения
аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке).
Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.
∆x – приращение аргумента
∆y – приращение функции
Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Главная линейная относительно Dх часть малого приращения функции называется дифференциалом функции и обозначается dy.
Приращением функции, соответствующим данному приращению аргумента, называется разность двух значений функции от соответствующих аргументов и обозначается Dу:
Dх=х-х0 , Dу=f(x)-f(x0).
Допустим, х – некоторая произвольная точка, которая лежит в какой-либо окрестности точки х0. Приращением аргумента в точке х0 называется разность х-х0. Обозначается приращение следующим образом: ∆х.
∆х=х-х0.
Функция одной переменной. Пусть задана функция у = f(x), определенная при значении аргумента, равном х0. Дадим аргументу приращение Dх, т.е. рассмотрим значение аргумента, равное x0 + Dх. Предположим, что это значение аргумента также входит в область определения данной функции. Тогда разность
Dy = f(x0 + Dх) – f(x0) называется приращением функции.
Если функция дифференцируема то она непрерывна, однако непрерывная функция не всегда дифференцируема.
Геометрическое и механическое истолкование производной.
Геометрический смысл производной: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке
Уравнение касательной: y = f ( x0 ) + f ’( x0 ) · ( x – x0 ) .
Механический смысл производной:
Скорость – это производная координаты по времени. v ( t0 ) = x’ ( t0 )
Ускорение – это производная скорости по времени. a = v’ ( t ).
