1. Що вивчає цифрова схемотехніка?

ЦС- галузь науки і техніки і виробництва, яка пов’язана з розробленням, дослідженням, проектуванням і виготовленням електронних схем, де перетворення та оброблення інформації відбувається за законом дискретної функції. ЦС вивчає принципи побудови та функціонування пристроїв ЦС, принципи вибору методів та аналізу розрахунку електронних пристроїв із заданими х-ками.

2. Логічні елементи і схеми. Принцип двоїстості

Відповідно до переліку логічних операцій розрізняють три основних логічшіх елементи (ЛЕ): і. АБО, НЕ.

Число входів елементів 1, АБО може бути довільним, а елемент НЕ мас завжди тільхи один внхід.

П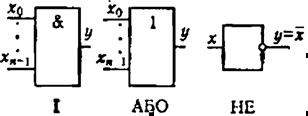 орівнявши операції І та АБО, можна дійти висновку, що якщо в умовах, які визначають операцію І, значення всіх змінних і самої функції замінити їх інверсісю, а знак логічн го множення — знаком логічного додавання, дістанемо посту-лати, що визначають операцію АБО:

Дві функції алгебри логіки називають двоїстими, якщо одна випливас з іншої заміною кожної операції кон'юнкції на операцію диз'юнкції і навпаки.

Важливим практичним наслідком принципу двоїстості є той факт, що при записі логічних виразів і, отже, побудові логічних схем можна скористатися тільки двома типами операцій, наприклад операціями І та НЕ чи АБО та НЕ.

3. Класифікація логічних пристроїв за способом введення-виведен ня інфор­мації

Логічні пристрої можна класифікувати за різними ознака­ми. За способом введення-виведен ня інфор­мації логічні пристрої розподіляють на послідовні, пара­лельні і послідовно-паралельні.

Послідовним називають пристрій, з якому початкові змінні подаються на вхід, а скінченні змінні знімаються з виходу не одночасно, а послідовно, розряд за розрядом.

Паралельним називають пристрій, в якому всі розряди по­чаткових змінних подаються на вхід, а всі розряди скінчен­них змінних знімаються з ниходу одночасно.

У послідовно-паралельних пристроях початкові і скінченні змінні подані у різних формах — або на вхід змінні пода­ються послідовно символ за символом, а з виходу вони зніма­ються одночасно, або навпаки.

4. Класифікація логічних пристроїв за принципом дії

За принципом дії всі логічні пристрої розподіляють на два класи — комбінаційні і послідовні.

Комбінаційними пристроями, або автоматами без пам'яті, називають логічні пристрої, вихідні сигнали яких однозначно визначаються тільки діючою у певний момент на вході ком­бінацією змінних і не залежать від значень змінних, що діяли на вході раніше.

Послідовними пристроями, або автоматами з пам'яттю, на­зивають логічні пристрої, вихідні сигнали яких визначаються не тільки діючою у певний момент на вході комбінацією змінних, а зі усією послідовністю початкових змінних, шо дія­ли у попередні моменти часу.

5. Комбінаційна схема

Комбінаційну схему можна зобразити у вигляді m-k-по­люсного елемента . Вхідне слово (вхідний алфа­віт) комбінаційної схеми задають набором символів М = m1m2..mi, а вихідне слово (вихідний алфавіт) набуває зна­чення з вихідних символів К =k1k2..ki

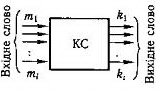
У дискретний момент часу сукупність вихідних сигналів однозначно визначають набором вхідних сигналів, що надхо­дять на вхід у той самий момент часу. Комбінаційна схема характеризується: числом вхідних сигналів, числом вихідних сигналів, логічною формулою або таблицею істинності.

6. Подання інформації у цифрових ЕОМ.

7. Перемикальна, Булева функція

Функція f, яка залежить від n змінних x1, x2, …,xn, називається булевою або перемикальною, якщо сама функція та її аргументи приймають значення тільки з множини {0, 1}. Аргументи булевої функції також називаються булевими. Довільна булева функція задається одним із трьох способів: матричним (табличним), геометричним та аналітичним.

Алгебра логіки дає. змогу створювати складні функції, аргументи яких є функціями інших двійкових аргументів. Операцію заміни аргументом однієї функції іншими, більш простими функціями називають суперпозицією функції. Багаторазове використання принципу суперпозиції дає можливість дістати функції бажаного числа аргументів.

Елементарна кон'юнкція утворюється кон'юнкцією скінчен-ної множини логічних змінних і їх заперечень.

Е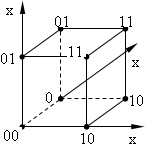 лементарна диз'юнкція утворюється диз'юнкцією скінченної множини логічних змінних і їх заперечень.

8. Геометричний спосіб задання функції

Геометричний спосіб задання функції – задання булевої функції f(x1, x2, …, xn) за допомогою n-вимірного куба. В геометричному розумінні кожен двійковий набір є n-вимірним вектором, який визначає точку n-вимірного простору. З цього випливає, що вся множина наборів, на яких визначена функція n змінних, може бути представлена вершинами n-вимірного куба. Позначаючи точками вершини куба, в яких функція приймає одиничне (або нульове) значення, отримаємо геометричне зображення функції.

9. Аналітичне подання функцій.

Булеві функції, що залежать від великої кількості змінних, задавати таблицею істинності незручно через її громіздкість. Наприклад, таблиця істинності функції 8 змінних матиме 2⁸ = 256 рядків. Тому для задання функції багатьох змінних зручніше використовувати модифікацію таблиці істинності.

Аналітичний спосіб – це задання функції за допомогою формул, тобто аналітичних виразів, побудованих на основі операцій булевої алгебри. Аналітичний спосіб задання булевих функції має особливе значення при проектуванні цифрових автоматів. Фактично всі перетворення над булевими функціями, необхідні для побудови цифрових автоматів, проводяться на аналітичному рівні.

10. Т аблиця істинності.

При визначенні матричним способом булеву функцію f (x1, x2, …,xn) задають таблицею істинності. В її лівій частині представлені всі можливі двійкові набори довжини n, а в правій вказується значення функції на цих наборах.

Під двійковим набором розуміють сукупність значень аргументів x1, x2, …,xn булевої функції. Двійковий набір має довжину n, тобто представлений n цифрами з множини {0, 1}. В табл.. перераховані всі двійкові набори довжини 3.

11. Булева алгебра

Для булевої алгебри визначені одна одномісна (унарна) операція «заперечення», дві двомісні (бінарні) операції кон‘юнкція та диз‘юнкція (позначаються “•” і “V” відповідно).

В цій алгебри справедливі три аксіоми:

закон комутативності — ;

закон асоціативності — ;

закон дистрибутивності — .

12. Функції одного аргументу.

Таких функцій чотири: f 1-f4, але на практиці працюють тільки з однієї - з f 1, що називають запереченням (інверсією).

а	f1 (-ф)	f2(a)	f3 (логичесна 1)	f4 (логичний 0)
0	1	0	1	0
1	0	1	1	0

13. Функції двох аргументів.

Таких функций уже шестнадцать (табл. 4.3).

Таблица 4.3. Двоичные функции двух двоичных аргументов

а	b		f1 (^)		f2				f3 ( - )		f4			f 5 ( > )				£6 ( < )				f7 ( v )			f8 (|)
0	0		0		0				1		0			1				1				1			1
0	1		0		1				0		1			0				1				0			1
1	0		0		1				0		1			1				0				0			1
1	1		1		1				1		0			1				1				0			0

а	b	f9	f10	f11	f12	f13	fl4	f15	f16
		(>)	(<)	( ¬a)	( ¬b)	(a)	(b)	(1)	(0)
0	0	0	0	1	1	0	0	1	0
0	1	0	1	1	0	0	1	1	0
1	0	1	0	0	1	1	0	1	0
1	1	0	0	0	0	1	1	1	0

Табл. 4.3 ділиться на дві частини: "іменну" (f 1- f 8) і безіменну (f 9- f 16). От імена перших восьми21 функцій:

- f 1 - конъюнкция (логічне множення), позначається:

- f 2 - диз'юнкція (логічне додавання), позначається: v, +, АБО, Or, | |,max;

- f 3 - рівнозначність (еквівалентність, тотожність), позначається:

- f 4 - нерівнозначність (нееквівалентність, розділова диз'юнкція, сума по модулі 2), позначається:

- f 5 і f 6 - імплікація (f 5 - імплікація від а до ь (позначається: - імплікація від b до а, логічне проходження (позначається:

- f7 - функція (стрілка) Пірса (функція Вебба, функція Даггера, антидиз'юнкція), позначається:

- f 8 - функція (штрих) Шеффера (антиконъюнкция), позначається:

Інші вісім функцій табл. 4.3 (f 9- f 16, як, втім, і три останні функції табл. 4.2) не мають ні імен, ні практичного застосування. Це або константи (f15 і f16), або функції тільки одного аргументу (f 11-f14-ім'я, та й то умовно, можна дати тільки функціям f9 і f 10 - інверсія імплікації.

14. ДНФ та КНФ.

Диз'юнкцію будь-якого числа елементарних кон'юнкцій називають диз'юнктивною нормальною формою (ДНФ).

Кон'юнкцію будь-якого числа елементарних диз'юнкцій називають кон'юнктивною нормальною формою (КНФ).

Логічну функцію, задану будь-яким аналітичним виразом, можна безпосередньо перетворити на нормальну диз'юнктивну (або кон'юнктивну) форму. Для нього потрібно:

виразити всі операції через операції кон'юнкції, диз'юнкції та інверсії;

позбутися інверсії над цілими виразами, перейшовши до форми, в якій є інверсії тільки окремих змінних;

розкрити дужки, застосувавши закон дистрибутивності;

звести кон'юнкції (диз'юнкції) до елементарних операцій.