11 вопрос

Теоре́ма об измене́нии коли́чества движе́ния (и́мпульса) систе́мы — одна из общих теорем динамики^[1], является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь в теореме, может выступать любая механическая система, состоящая из любых тел

Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы.

Пусть система состоит из   материальных точек с массами   и ускорениями  . Все силы, действующие на тела системы, разделим на два вида:

• Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим  .

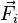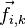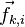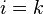• Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать  , а силу воздействия i-й точки на k-ю точку —  . Очевидно, что при  , то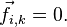 

Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде

Учитывая, что   и суммируя все уравнения второго закона Ньютона, получаем:

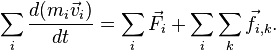
Выражение   представляет собой сумму всех внутренних сил, действующих в системе. По третьему закону Ньютона в этой сумме каждой силе   соответствует сила   такая, что   и, значит, выполняется   Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать

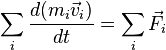
Используя для количества движения системы   обозначение  , получим

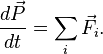
Введя в рассмотрение изменение импульса внешних сил  , получим выражение теоремы об изменении количества движения системы в дифференциальной форме:

Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми   и  , получим выражение теоремы об изменении количества движения системы в интегральной форме:

где   и   — значения количества движения системы в моменты времени   и   соответственно, а   — импульс внешних сил за промежуток времени  . В соответствии со сказанным ранее и введёнными обозначениями выполняется

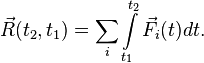
Вопрос 13

Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

 Для изучения вращательного движения твердого тела вокруг неподвижной оси воспользуемся теоремой об изменении момента количества движения (кинетического момента) механической системы относительно оси (3.10):

                                               dK_z/dt = M_z^e.                                            (3.11)

         Пусть на твердое тело, имеющее неподвижную ось вращения z (рисунок 3.4), действует система заданных внешних активных сил (F₁, F₂, F₃,...,F_n ), определяющих угловую скорость ω и угловое ускорение ε этого тела в его вращательном движении вокруг оси z. Одновременно на это же тело действуют силы реакции R_A подпятника иR_B радиального подшипника. 

         Определяем правую часть уравнения (3.11):

 M_z^e = ∑M_z(F_j^e) + M_z(R_A) + M_z(R_B).

         Поскольку M_z(R_A) = M_z(R_B) = 0, то M_вращ = M_z^e = ∑M_z(F_j^e).

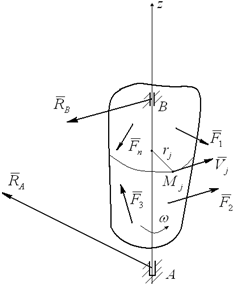
Рисунок 3.4

         Найдем момент количества движения (кинетический момент) K_z вращающегося твердого тела. Для этого выделим точку M_j тела на расстоянии r_j от оси вращения и имеющую скорость V_j = ω⋅r_j. Очевидно, что K_zj = m_j ⋅ V_j ⋅ r_j = m_j ⋅ω ⋅r_j². Тогда момент количества движения (кинетический момент) всего вращающегося тела будет:

 K_z = ∑K_zj = ∑m_j ⋅ω ⋅r_j²,

где ∑m_j ⋅r_j² = J_z.

         Следовательно, окончательно будем иметь

                                                 

                                       K_z = J_z ⋅ ω.                                             (3.12)

         Подставляя в уравнение (3.11)  выражение (3.12), получаем

 J_z ⋅ dω/dt = M_вращ,

или

                                             J_z ⋅d²φ/dt² = M_вращ.                          (3.13)

         Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

         Поскольку dω/dt = ε, имеем

                                              ε = M_вращ/J_z.                                      (3.14)

         Полученное выражение (3.14) показывает, что осевой момент инерции J_z тела следует рассматривать как меру инертности твердого тела при его вращательном движении вокруг неподвижной оси.

12 Вопрос

Вопрос 14

Элементарная работа силы

Для характеристики действия, оказываемого силой на тело  при его перемещении, существует понятие о работе силы.

Элементарной работой силы F приложенной в точке М называется скалярная величина

dA = F_ • dS,

г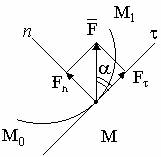 де F_  - проекция силы на касательную к траектории (направление скорости):

F_  = F•cos,

тогда

dA = F•ds cos..

При остром угле  работа положительна  (сила  помогает  движению); если  - тупой, работа  отрицательна  (мешает  движению); при  = 90⁰  работа равна нулю  (не влияет на движение)

Если учесть, что  dS = dr, где dr -  вектор элементарного перемещения точки, то элементарная работа равна скалярному произведению двух векторов:

.

Элементарная  работа силы равна скалярному произведению вектора силы на вектор элементарного перемещения точки её приложения.

Т.к. r_x = x; r_y = y; r_z = z, то аналитическое выражение работы:

  .