Законы распределения случайных величин

Закон распределения вероятностей получения значений случайных величин в процессе эксперимента – это любое соотношение между случайными величинами и вероятностями их появления. Закон распределения бывает нескольких форм:

1. числовой ряд – получается в процессе проведения эксперимента. В этом случае закон распределения для практического применения не годится. Это – «сырье», которое дает результат при дальнейшей обработке, исходный статистический материал.

2. вариационный ряд – это то же самое, только значения в нем упорядочены.

3. таблица – каждой величине соответствует вероятность ее появления:

Случайная величина Xi	X1	X2	X3	…	Xn
Вероятность ее появления	p1	P2	p3	…	Pn

В таком виде представить зависимость неудобно, поэтому иногда пользуются укрупненными графиками.

Ч асто на основании многоугольника распределения строят гистограмму. Для многих исследований гистограммы являются результатом.

4. график – используется, когда имеется много статистического материала.

Ф ункция распределения вероятностей значений случайной величины – это вероятность того, что случайная величина примет значение, меньшее некоторого фиксированного, наперед заданного, числа.

X₁, X₂,…,X_n – генеральная совокупность;

R – некоторое число.

Г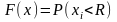 рафически функция распределения F(x) – это вероятность того, что случайная величина X_i займет точку левее R:

F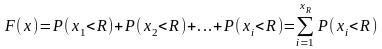 (x) принимает столько значений, сколько реализаций имеет случайная величина.

x_R – последнее значение x_i, меньшее R.

Рассмотрим график F(x) для дискретных СВ. Пусть имеется таблица:

Xi	x1	x2	x3	x4	x5
Pi	p1	p2	p3	p4	p5

Д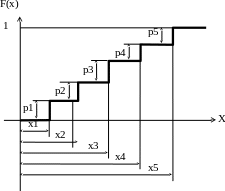 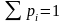ля нее график – ломаная линия:

П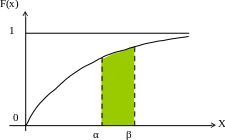 рактически важной ситуацией является случай, когда необходимо определить вероятность попадания случайной величины в интервал значений. В этом случае вероятность будет равна разности функций распределения на концах этого интервала.

График функции F(x) непрерывных случайных величин:

Вероятность попадания вероятности СВ в заданный интервал от α до β:

Ф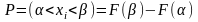 ункция распределения справедлива как для дискретных, так и для непрерывных СВ.

Плотность распределения вероятностей значений СВ представляет собой производную от функции распределения: .

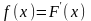Пусть имеется некоторая СВ X, которая принимает значения x₁, x₂,…, x_n и имеет функцию распределения F(X). Вероятность попадания вероятности СВ в интервал Δx: . Разделим это выражение на Δx:

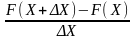
– вероятность, приходящаяся на единицу этого интервала

П лотность вероятностей – это отношение разности функций распределения на границах интервала к величине этого интервала, т.е. вероятность, приходящаяся на каждую единицу интервала.

– вероятность попадания СВ в интервал (α,β).

График плотности распределения вероятностей:

Б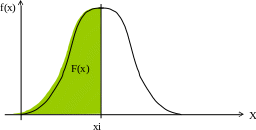 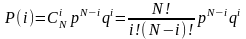иномиальный закон распределения вероятностей:

p – вероятность появления события;

q = 1–p – вероятность появления обратного события.

Условие применимости биномиального закона распределения – он позволяет определить вероятность появления одного или двух событий.

Распределение Пуассона: 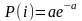, где a – параметр распределения, который представляет собой среднюю вероятность появления события за время испытания.

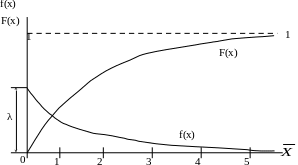
Экспоненциальное распределение: 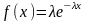, где λ – параметр, учитывающий специфику изделий данного типа; f(x) – плотность вероятностей появления СВ x.

Для экспоненциального распределения λ = const, которая для каждого типа аппаратуры определяется путем статистических испытаний.

Свойство этого распределения – оно не зависит от начала отсчета времени.

– нормированное значение в относительных единицах, т.е. интервал, в течение которого вероятность события уменьшается в e раз.

З акон распределения Гаусса:

σ – среднеквадратическое отклонение;

M(x) – математическое ожидание.

Область применения – потоки отказов постепенного характера, статистический контроль качества.