Плоский случай
Задана точка
в относительной системе координат и
положение относительной системы
координат в абсолютной системы, которое
определяется вектором смещения точек
начала координат и углом поворота α.
Требуется вычислить координаты точки в абсолютной системе
,
(6.7)
где
(6.8)
Рисунок 6.11
Орты
в абсолютной системе координат
определяются таким образом
(6.9)
Знак угла α является положительным, если поворот совершается против часовой стрелки.
Подставляя соотношения (8) в (7) после соответствующих преобразований, получим
.
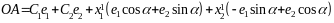(6.10)
Приравнивая координаты при
в правых и левых частях (10), получаем
связь между абсолютными и относительными
координатами точки А:
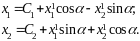(6.11)
Соотношения (11) можно записать в матрично-векторной форме:
(6.12)
Матрица для плоского случая имеет
размерность (3×3), ее можно представить
в виде произведения матрицы
-
матрицы параллельного переноса начала
относительной системы координат на
величину вектора
и матрицы поворота относительной
системы координат относительно абсолютной
:
,
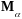(6.13)
где
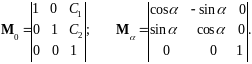(6.14)
Обратная матрица преобразований
(6.15)
Пространственный случай
Для пространственного случая матрица
преобразований
строится по аналогии с плоским случаем,
предполагая, что переход от относительной
системы координат к абсолютной получается
в результате последовательных движений:
- параллельного
переноса вдоль вектора
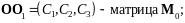
- поворота
осей координат абсолютной системы
соответственно
на углы
- матрицы поворота
.
Существенное значение имеет последовательность движений:
(6.16)
.
После перемножения матриц , матрица преобразования примет вид
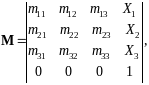(6.17)
где
Обратная
матрица
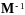имеет
вид
(6.18)
Обратная матрица поворота - это тоже матрица поворота вокруг той же оси на тот же угол поворота, но в отрицательном направлении; она получается из матрицы поворота путем транспонирования, то есть
.
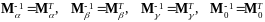Например,
и т.д.