Пространственный случай описания детали

При построении базового множества М для трехмерных деталей возникают технические трудности определения уравнений поверхностей в трехмерном пространстве в случае произвольной ориентации их относительно координатных осей. Ввиду того, что логико-алгебраическое описание деталей предполагает аналитическую форму представления поверхностей, то это представление будем называть внутренним. Для пользователя более удобным является кодирование параметров поверхностей на основе использовании информации с чертежа, которая полностью определяет уравнение рассматриваемой поверхности. Такую форму представления поверхностей называют внешней. Внешнее представление поверхности зависит от ее вида: плоскость, цилиндрическая, коническая, сферическая, тороидальная, составная поверхность.

Рассмотрим возможности внешнего представления перечисленных выше поверхностей, которые имеют наибольшее распространение при образовании машиностроительных деталей.

Плоскость.

Плоскость в трехмерном пространстве определяется тремя точками, не лежащими на одной прямой. Возможны различные способы внешнего представления плоскости.

1. Заданы три точки не лежащие на одной прямой, которые в совокупности определяют девять параметров плоскости. Координаты точек могут быть получены чертежа. Например, плоскость скоса π (рисунок 6.4) призматической детали определяются точками

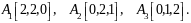
Рисунок 6.4

2. Заданы точка и нормаль к плоскости в точке А. Плоскость скоса призматической детали D определяется шестью параметрами: тремя координатами точки А и тремя направляющими косинусами нормали (рисунок 6.5).

Рисунок 6.5

3. Частные случаи расположения плоскости параллельно координатным плоскостям . В этом случае параметры плоскости

Определяются непосредственно коэффициентами ее уравнения. Например, уравнение плоскости, параллельной координатной плоскости и смещенной на две единицы по координате (рисунок 6.6) будет иметь вид:

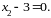
Рисунок 6.6

Цилиндрическая поверхность

Цилиндрическая поверхность в трехмерном пространстве определяется семью параметрами: координатами двух несовпадающих точек на оси вращения цилиндра и радиус окружности пересечения цилиндрической поверхности и плоскости, перпендикулярной оси вращении (рисунок 6.7)

Рисунок 6.7

Сферическая поверхность

Сферическая поверхность определяется четырьмя параметрами – тремя координатами центра и радиусом R (рисунок 6.8)

Рисунок 6.8

Тороидальная поверхность

Тороидальная поверхность (рисунок 6.9) определяется восемью параметрами: три координаты центра большой окружности и его радиус R; радиус малой окружности r и три направляющих косинуса нормали к плоскости центров.

Рисунок 5.9

Коническая поверхность

Коническая поверхность определяется восемью параметрами: шесть координат центров оснований А₁ , А₂ , радиусов R₁ , R₂ окружностей пересечения плоскостей, проходящих через точки А₁ , А₂ и перпендикулярных оси вращения конической поверхности (рисунок 6.10)

Рисунок 6.10

Поверхность общего вида может быть получена в результате аппроксимации сплайнами, в частности, сплайнами второго порядка.

Преобразование из внешнего представления во внутреннее.

Для получения аналитического уравнения поверхности П на основе параметров ее внешнего представления используется матрица М преобразования координат из относительной системы в абсолютную.

Преобразование производится в следующей последовательности.

1. Выбор собственной системы координат, связанной с поверхностью П.

2. Получение уравнения поверхности П в собственной системе координат:

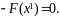
3. Вычисление матрицы М преобразования координат: на основе внешнего представления поверхности.

4. Вычисление обратной матрицы М^-1 преобразования координат:

5. Пересчет уравнения поверхности в абсолютную систему координат с учетом матрицы М^-1 преобразования координат:

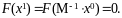
Рассмотрим матрицы М преобразования координат из относительной системы в абсолютную для плоского и пространственного случаев и расчет обратной матрицы М^-1.