Пересечение множеств

Пересечением множеств X и Y называется множество, состоящее из всех тех элементов и только тех, которые принадлежат как множеству Х, так и множеству Y,

Рисунок 2.2

то есть пересечение множеств, есть множество состоящее из элементов, общих для обеих множеств X, Y.

Пересечение множеств обозначается знаком « ». Формальное определение пересечения множеств

(2.8)

Пересечение множеств иногда называют произведением множеств и обозначают .

Множества X и Y называются непересекающимися, если они не имеют общих элементов (рисунок 3), т. е.

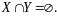
Рисунок 2.3

Если задано множество М множеств Х_i , т.е. , пересечение этих множеств записывается так

. (2.9)

и представляет собой множество элементов, общих для всех множеств Х_i.. Имее5т место также соотношение

Разность множеств

Разностью множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат Х и не принадлежат Y (рисунок 4)

Рисунок 2.4

Разность множеств обозначается знаком «\»:

. (2.10)

Универсальное множество

. (2.11)

Соотношение (11) означает, что пересечение или «общая часть» множества I и множества Х для любого множества Х совпадает с самим этим множеством. Но это возможно лишь в том случае, если множество I содержит все элементы, из которых может состоять множество Х, так что любое множество Х полностью содержится в множестве I. Множество I играет роль единицы (как в обычной алгебре ).

Множество I, удовлетворяющее этому условию называется универсальным или полным.

Универсальное множество удобно графически представлять в виде прямоугольника

Рисунок 2.5

Различные области внутри этого прямоугольника будут представлять различные подмножества универсального множества.

Универсальное множество обладает свойством, не имеющем аналогов в обычной алгебре

. (2.12)

Дополнение множества

Множество , определяемое из соотношения

, (2.14)

называется дополнением множества Х (до полного множества I )

Рисунок 2.6

Из (14) следует, что если и не имеют общих элементов

(2.15)

Кроме того, не имеется элементов I, которые не принадлежали бы ни , ни , так как те элементы, которые не принадлежат , принадлежат

(2.16)

Из (15) и (16) следует, что

. (2.17)

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является разбиение множества на систему подмножеств.

Пусть задано множество М и система множеств . Систему множеств Т называют разбиением М, если удовлетворяются следующие условия:

1. любое множество Х из Т является подмножеством множества М:

;

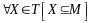2. любые два множества X и Y из Т являются непересекающимися:

3. объединение всех множеств, входящих в разбиение, дает множество М:

Упорядоченные множества

Кортежом или упорядоченным множеством называется последовательность элементов, т.е. совокупность элементов, в которой каждый элемент занимает определенное положение. Сами элементы при этом называются компонентами кортежа (первый компонент, второй компонент и т.д.), Примеры кортежей: множество людей, стоящих в очереди; множество слов в фразе; долгота и широта точки на местности; множество солдат, идущих строем и т.п. Во всех этих приметах место каждого элемента вполне определенно и не может быть произвольно изменено. Часто в технических задачах часто эта определенность является предметом договоренностей.

Число элементов кортежа называют его длиной. Для определения кортежа используются круглые скобки

Кортежи длиной в 2 элемента называются парами или упорядоченными парами; длиной 3 – тройками и т.д. В общем случае кортежи длиной п называют п-картами. Частным случаем кортежа является кортеж (а) длиной 1 и пустой кортеж длиной 0, обозначаемый ( ) или Λ. В отличии от обычного множества в кортеже могут быть и одинаковые элементы.

Для нас большое значение имеют упорядоченные множества, элементами которых являются действительные числа. Такие упорядоченные множества называются точками пространства или векторами. Так, кортеж (а1, а2) может рассматриваться как точка плоскости или вектор, проведенный из начала координат в точку с координатами (а1, а2). Тогда компоненты кортежа а1 и а2 будут проекциями вектора на оси 1 и 2

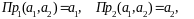
или в общем виде

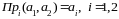
Кортеж (а1, а2, а3) может рассматриваться как трехмерный вектор. Тогда

Обобщая понятие вектора, можно рассматривать упорядоченное п-элементное множество вещественных чисел

как точку в воображаемом п-мерном пространстве или п-мерным вектором. При этом компоненты п-элементного кортежа будем рассматривать как проекции этого кортежа на соответствующие оси

_(2.18)

Ели множество конечно, то

Если множество упорядоченно, то вводится прямое произведение множеств. Прямым произведением множеств Х и Y называется множество, обозначаемое X×Y и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству Х, а вторая – множеству Y. Прямое произведение обозначается

. (2.19)

Прямое произведение не обладает свойством коммутативности

Прямое произведение двух множеств может быть легко обобщено на случай большего числа множество. Прямым произведением множеств называется множество, обозначаемое и состоящее из всех тех и только тех кортежей длины п, первый элемент которых принадлежит Х₁, вторая – Х₂ и т.д. Частным случаем прямого произведения является понятие степени множества. Пусть М произвольное множество. s-ой степенью множества М называется прямое произведение s одинаковых множеств М.

Проекция множества

Операция проектирования множества тесно связана с операцией проектирования кортежа и может применяться только к тем множествам, элементами которых являются кортежи одинаковой длины.

Пусть М – множество, состоящее из кортежей одинаковой длины s. Тогда проекцией множества М называется множество проекций кортежей из М.

Если , то

Пр₁М=Х, Пр₂ М=Y, (2.20)

а если то

. (2.21)

Соответствия

Рассмотрим два множества X и Y. Элементы этих множеств могут каким либо образом сопоставляться друг и другом , образуя пары (х,y). Если способ такого сопоставления определен, то есть для каждого элемента 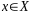указан элемент , с которым сопоставляется элемент х, то говорят, что между множествами X и Y установлено соответствие. При совершенно необязательно, чтобы в сопоставлении участвовали все элементы множеств X и Y, важно указать закон, в соответствии с которым осуществляется соответствие, т.е. перечисляющее все пары (х,y), участвующие в сопоставлении. Соответствие обозначается буквой «q», представляет собой тройку множеств

,

в которой В этом выражении первую компоненту Х называют областью отправления соответствия, вторую компоненту Y – областью прибытия соответствия, третью компоненту Q – графиком соответствия. 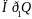Кроме этих множеств, с каждым соответствием неразрывно связаны еще два множества:1) множество , называемое областью определения соответствия, в которую входят элементы множества , участвующие в сопоставлении; 2) множество называемое областью значений соответствия, в которую входят элементы множества , участвующие в сопоставлении.

Если , то говорят, что элемент у соответствует элементу х.

Для каждого соответствия существует обратное соответствие

(2.22)

Последовательное применение двух соответствий называется композицией соответствий

(2.23)

Причем область значений первого соответствия совпадает с областью значений второго соответствия:

Композицию соответствий q и p обозначается q(p), а график композиции - . При этом композиция соответствий (23) запишется в виде