Лекция 2 ММ ТП в маш.

Элементы теории множеств

Множество – совокупность объектов, объединенных каким-либо общим признаком. Отдельные объекты, из которых состоит множество, называются элементами множества. О множестве элементов можно говорить только тогда, когда эти элементы различимы между собой.

Общим обозначением множества служат фигурные скобки , внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используются прописные буквы латинского алфавита , для обозначения элементов множества используется строчные буквы , или строчные буквы с индексами

Для указания того, что некоторый элемент, а принадлежит множеству S используется знак « ». Запись означает, что элемент а принадлежит S, а запись означает. что элемент а не принадлежит множеству S. Записью пользуются для сокращения записи

Множества бывают конечными и бесконечными. Множество называется конечным, если число его элементов конечно, т.е. если существует такое натуральное число N, являющееся числом элементов множества и бесконечным, если оно содержит бесконечное число элементов.

Чтобы оперировать с конкретными множествами нужно их задавать. Существует два способа задания множеств:

а) задание множества способом перечисления всех элементов, составляющих множество;

б) задание множества описанием общего признака, которым обладают элементы множества.

Способом перечисления обычно задаются конечные множества. Так, например, множество отличников в группе можно задать, перечислив пофамильно всех студентов, учащихся на отлично. Для сокращения записи иногда пишут , или вводят множество индексов и пишут . Задание множества способом задания общего признака элементов состоит в том, что указывается этот признак. Например, множество отличников группы в виде 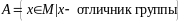. В тех случаях, когда не вызывает сомнений, из какого множества берутся элементы х, указание о принадлежности элемента х к множеству М можно не делать: . Примеры задания множеств способом указания общего признака:

- множество четных чисел; 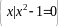- множество .

Пусть С – множество целых чисел. Тогда есть множество .

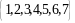Пустым множеством называется множество , не содержащее ни одного элемента и обозначается через . Например, . Пустое множество относится к конечным множествам. Понятие пустого множества играет важную роль при задании множеств способом описания. Так, например, без понятия пустого множества мы не могли бы говорить о множестве отличников группы, не убедившись предварительно, есть ли вообще в группе отличники. Введение пустого множества позволяет совершенно спокойно оперировать со множеством отличников в группе, не заботясь о том, есть ли вообще в рассматриваемой группе отличники.

Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют одно и тоже множество. Множества не равны , если либо в множестве есть элементы, не принадлежащие , либо в есть элементы, не принадлежащие . Символ равенства обладает свойствами

1. рефлексивность;

2. если симметричность;

3. если - транзитивность.

Из определения множества вытекает, что порядок элементов в множестве несущественен, то есть, например, . Из определения же следует, что в множестве не должно быть неразличимых элементов, то есть запись некорректна и ее следует заменить на .

Понятие подмножества

Множество Х является подмножеством множества У, если любой элемент множества Х является элементом множества У.

В теории множеств применяются специальные символы. Для определения подмножества применяются два таких символа :

символ, называемый «квантор» и означающий любой, какой бы ни был, «для всех»;

символ следствия (импликации), означающий «влечет за собой».

Определение подмножества, которое может быть сформулировано в виде: для любого х утверждение «х принадлежит Х» влечет за собой утверждение «х принадлежит У» запишется так:

.

Более краткой записью выражения «Х является подмножеством У» будет запись

,

что читается как «Y содержит Х». Символ означает включение, а строгое включение, которое применяется тогда, когда хотят подчеркнуть, что множество содержит и другие элементы, кроме элементов из Х, т.е. . Связь между символами 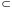и дается выражением

и .

Здесь использован знак , означающий эквивалентность, т.е. «то же самое, что».

Свойства подмножества:

1. рефлексивность – «множество Х является подмножеством самого себя»;

2. транзитивность – «если Х есть подмножество Y, а Y есть подмножество Z, то Х есть подмножество Z ».

3. для любого множества М.

Взаимно однозначное соответствие между множествами

Зачастую приходится сопоставлять элементы множеств. Если каждому элементу множества Х поставлен в соответствие элемент множества Y , то такое попарное соответствие между элементами двух множеств называется взаимно однозначным соответствием.

Пусть Х и Y два конечных множества, соответственно т- и п- элементные.

Между ними можно установить взаимно однозначное соответствие только в том случае, когда т = п. Для двух п – элементных множеств число взаимно однозначных соответствий будет

Множество можно разбить на подмножества различными способами. Общее число к-элементных подмножеств п-элементного множества М равно

, (2.1)

т.е. равно числу сочетаний из п элементов по к.

Общее число L всевозможных подмножеств п-элементного множества М равно

(2.2)

Счетные и несчетные множества

Если бесконечное множество возможно привести во взаимно однозначное соответствие с натуральным рядом, то такое множество называется счетным множеством. Если такое соответствие привести нельзя, то множество называется несчетныим.

Примеры счетных множеств.

1. Множество М квадратов целых чисел: 1, 4, 9, 16, … представляет собой лишь подмножество множества натуральных чисел, Однако множество М является счетным множеством, так как приводиться во взаимно однозначное соответствие с натуральным рядом, квадратом которого он является.

2. Счетным является множество С всех целых чисел – положительных и отрицательных, хотя натуральный ряд представляет собой только положительное подмножество этого множества

Из которого следует, что

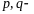3. Счетным является множество всех рациональных чисел где любые целые числа. Чтобы убедиться в этом, представим все множество рациональных чисел в виде таблицы, в которую заносим несократимые дроби

Обходя таблицу по направлению стрелок, приходим к последовательности

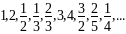
позволяющей занумеровать эти числа.

Теорема. (Г.Кантор) Множество всех действительных чисел интервала 0 < x ≤ 1

несчетно. Равносильное утверждение: множество всех точек интервала (0,1] несчетно. Рассмотренный интервал (0,1] может быть приведен во взаимно однозначное соответствие с любым интервалом (a, b] (например, с помощью центральной проекции). Отсюда, множество всех действительных чисел любого интервала (a, b] несчетно.