Уравнение Пуассона

Одними из распространенных параметров ориентации, используемых в бесплатформенных системах ориентации и навигации, являются направляющие косинусы (directional cosines). Девять косинусов углов между шестью осями ко­ординат однозначно определяют их взаимную ориентацию.

При принятой ранее последовательности поворотов ЛА на углы и переходе от связанной с ЛА системы координат к географической OX_sY_sZ_g получена матрица перехода С

(17)

Метод определения направляющих косинусов через углы последовательных поворотов приводит к необходимости вычисления произведений двух или трех функций синусов и косинусов угловых параметров ориентации, что представля­ет достаточно сложный и громоздкий процесс. Поэтому направляющие косину­сы чаще используются в качестве самостоятельных параметров ориентации, поскольку они могут быть вычислены аналитически, если известны их начальные значения и угловые скорости с которыми система OXYZ вращается относительно осей системы OX_eY_sZ_g. Если матрица (17) известна, то углы рыскания, тангажа и крена определяются через ее элементы:

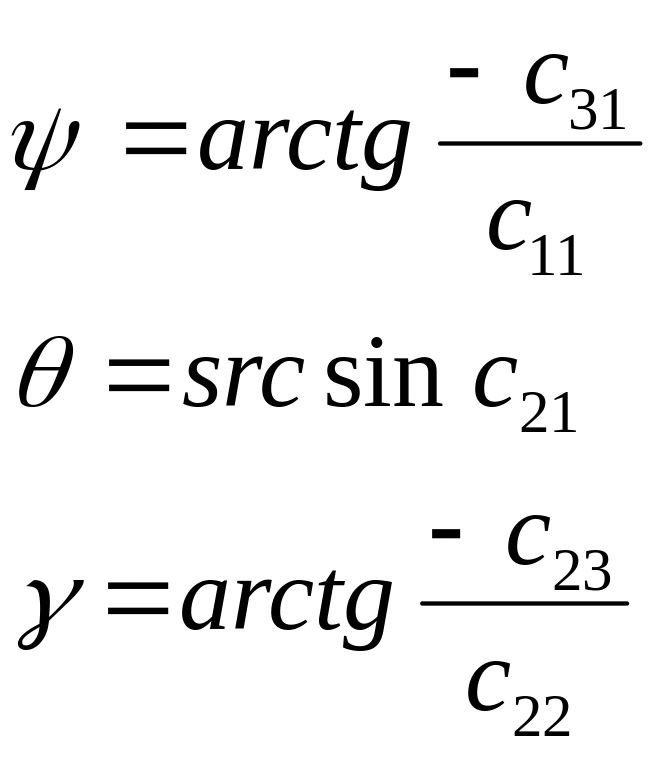(18)

Рассмотрим способы вычисления матрицы направляющих косинусов. Из теоретической механики известно, что дифференцирование вектора г , опре­деляющего координаты точки в некоторой системе координат OXYZ , дает линейную скорость

(19)

с проекциями на оси OXYZ.

Если эта система координат вращается с угловой скоростью с относительно некоторой неподвижной системы координат , то абсолютная линейная скорость точки определяется следующим образом

В правой части равенства (3.34) первое слагаемое, отмеченное знаком «~», представляет собой скорость точки в системе координат OXYZ, а второе учи­тывает факт вращения этой системы относительно неподвижной системы координат .

Векторному уравнению (3.34) соответствуют три скалярные, определяющие проекции вектора v абсолютной линейной скорости точки на оси подвижной системы OXYZ в виде

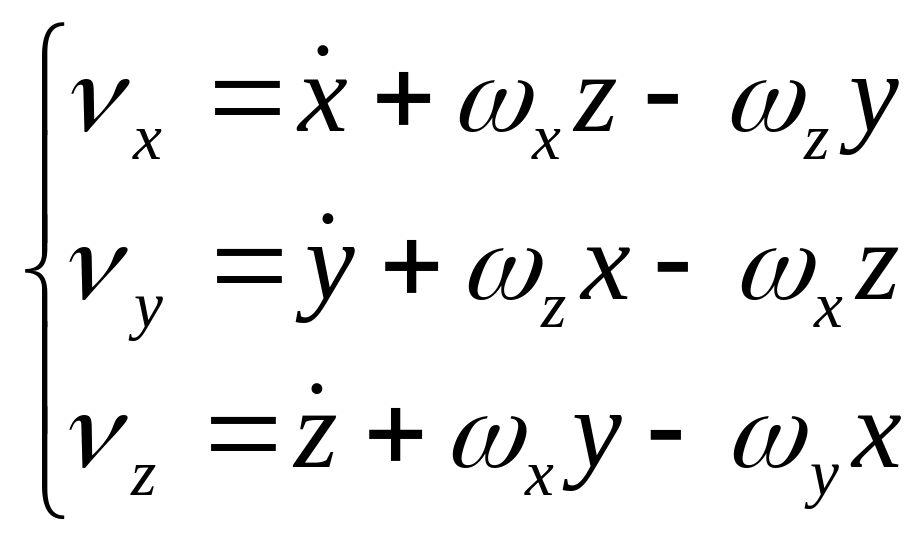(21)

В матричном виде операция дифференцирования вектора r по времени в системе координат определяется выражением

(22)

Где - координаты точки в системе координат

Дифференцирование вектора r во вращающейся системе координат OXYZ представляется так:

(23)

Векторному произведению в матричной форме записи соответствует произведение кососимметрической матрицы

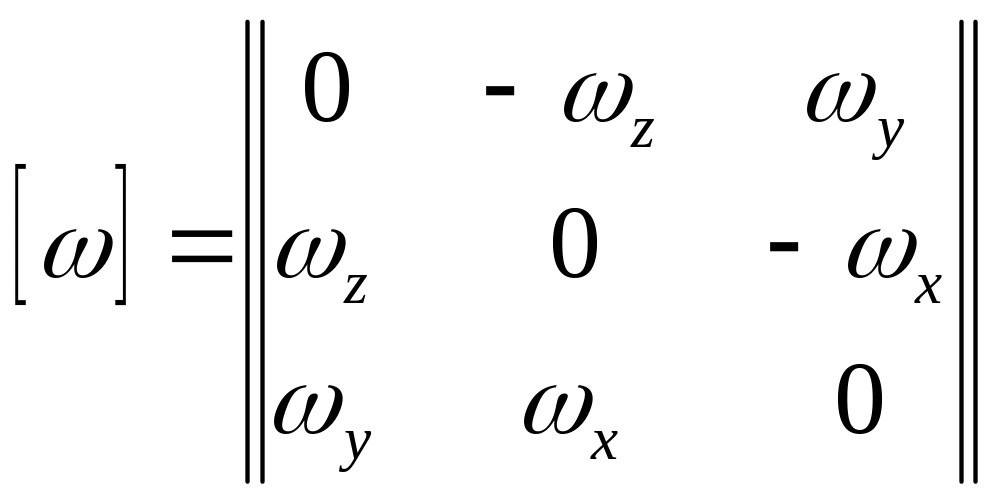(24)

на матрицу-столбец

(25)

Поэтому уравнение (21) можно переписать в матричной форме

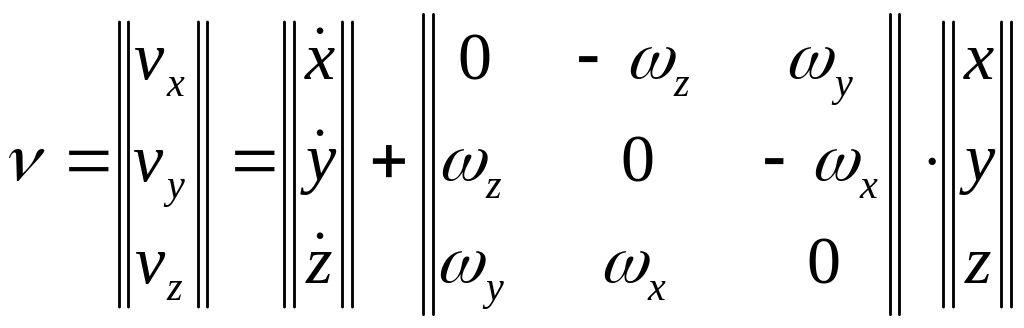(26)

Координаты точки в подвижной и неподвижной системах координат связаны матричной зависимостью

(27)

которая характеризует преобразование координат, т.е. переход от координат точки в неподвижной системе координат , к координатам той же точки в подвижной системе координат OXYZ. Матрица А с элементами (i,j = 1,2,3) характеризует именно этот переход.

При обратном переходе от координат точки в системе OXYZ к координатам в системе используется матрица С = А^Т, транспонированная по отношению к матрице А .

r=Cr^’

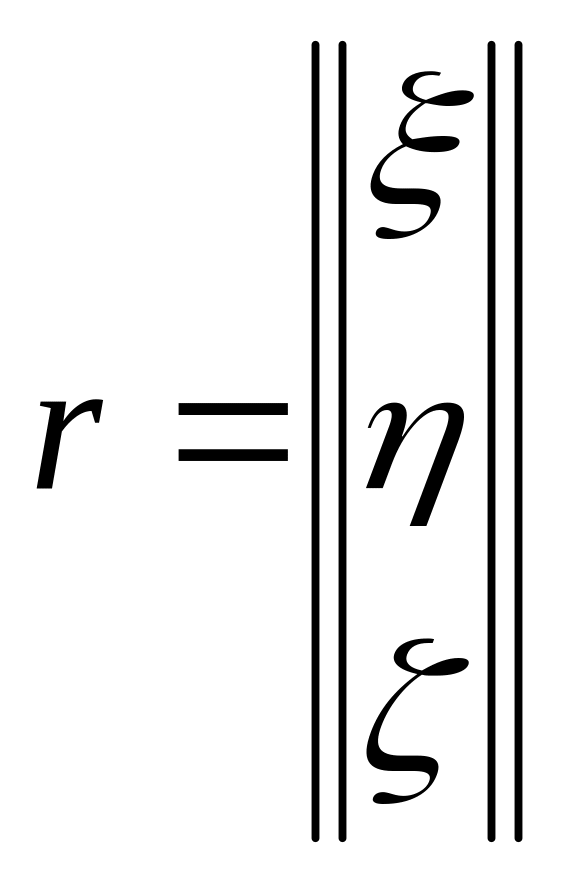матрица столбец из координат точки в системе , - то же в системе OXYZ, С - матрица преобразования координат при переходе от системы OXYZ к системе .

Для установления связи направляющих косинусов с угловыми скоростями , с которыми подвижная система координат вращается относительно неподвижной, продифференцируем по времени выражение (27)

r = Cr+Cr'. (28)

Умножим обе части равенства (3.43) на матрицу А и, учитывая, что

АС=Е, (29)

где Е -единичная матрица, перепишем уравнение (28) в виде

Ar = r' + ACr'. (30)

В уравнении (30) левая часть Аr представляет собой абсолютную линейную скорость точки v в подвижной системе координат, вследствие чего уравнения (2.40) и (2.45) эквивалентны. Из их сравнения следует, что

АС= или С=С . (31)

Уравнение (3.47) хорошо известно в теории инерциальной навигации как матричное дифференциальное уравнение Пуассона, связывающее производную от матрицы направляющих косинусов с самой матрицей и вектором угловой скорости , с которыми система OXYZ вращается относительно неподвижной ,.

Таким образом, если имеется информация о проекциях вектора абсолютной угловой скорости, на оси подвижной системы координат OXYZ, в виде -,, то направляющие косинусы по отношению к неподвижной системе координат могут быть рассчитаны путем интегрирования матричного уравнения Пуассона

(32)

Матричное уравнение эквивалентно девяти уравнениям первого порядка

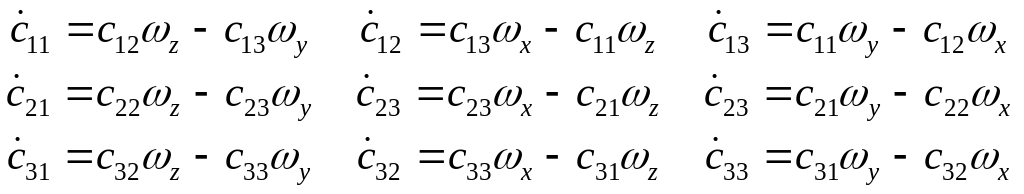(33)

Скалярный вид уравнения Пуассона показывает, что совокупность (3.50) распадается на три отдельно интегрируемые системы (триады) из трех уравнений каждая. Первая триада имеет переменные с_11, с_12, с₁₃, вторая – с₂₁, с₂₂, с₂₃, третья- с_31, с₃₂, с₃₃ .