Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Теоретические основы измерительных и информационных технологий.

Расчетно графическая работа

Расчет фильтра высоких частот

Задание 2 Вариант №7

Выполнил ст.гр.П-313СФ

Забродин В.В

Проверил:

Колегаев.Ю.Б

Уфа - 2015

Содержание

Введение

Задание

1. Теоретическая часть

1.1 Классификация фильтров

1.2 Аппроксимация активных фильтров

2. Расчетная часть

2.1 Реализация активного фильтра Баттерворта по схеме с ИНУН

2.1.1 Расчет порядка фильтра Баттерворта

2.1.2 Расчет элементов

2.1.3 Выбор ОУ

2.2 Реализация активного фильтра Чебышева по схеме с ИНУН

2.2.1 Расчет порядка фильтра Чебышева

2.2.2 Расчет элементов

2.2.3 Выбор ОУ

2.3 Результаты моделирования

Заключение

Список литературы

Введение

В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоте), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и полосно-заграждающие или режекторные фильтры ( которые задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).

Задание

Произвести расчет, используя полиномы Баттерворта и Чебышева, параметров активных фильтров низких частот (ФНЧ) или высоких частот (ФВЧ); по результатам расчета смоделировать работу фильтра (желательно использовать программу MicroCap). Представить результаты расчета в графическом виде (графики амплитудно-частотной характеристики (АЧХ) и фазо-частотной характеристики (ФЧХ)).

Задание №2, вариант №7:

1. Структуры:

а) ФВЧ Баттерворта по схеме источника напряжения управляемого напряжением;

б) ФВЧ Чебышева по схеме многопетлевой обратной связи;

2. Частота среза fс (кГц) – 15;

3. Частота f1, на которой происходит гарантированное затухание 30 дБ (кГц) – 3;

4. Коэффициент преобразования фильтра – 9.

1. Теоретическая часть

1.1 Классификация фильтров

Диапазоны и полосы частот, в которых сигналы проходят, называются полосами пропускания и в них значение АЧХ относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задерживания и в них значение АЧХ относительно мало, а в идеальном случае равно нулю. На рис. 1.1 штриховой линией показана АЧХ идеального фильтра нижних частот с единственной полосой пропускания и полосой задерживания 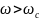. Частота между этими полосами определяется как частота среза.

Рис. 1.1 Идеальная и реальная АЧХ ФНЧ

Реализовать эту идеальную характеристику на практике невозможно, поскольку требуется сформировать очень узкую переходную область. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной реальной характеристики с заданной точность к идеальной.

Как только получена подходящая передаточная функция, разрабатывают схему фильтра, реализующую данную передаточную функцию. При этом разработка выливается в проектирование активных и пассивных фильтров.

Пассивные фильтры представляют собой устройства, которые создаются на основе резисторов, конденсаторов и катушек индуктивности, а именно из пассивных схемных элементов. Эти фильтры пригодны для работы в определенных диапазонах частот, но не подходят для низких частот, например ниже 0,5 мГц. Это происходит вследствие того, что на низких частотах параметры требуемых катушек индуктивности становятся неудовлетворительными из-за их больших размеров и значительного отклонения рабочих характеристик от идеальных и, кроме того, в отличие от резисторов и конденсаторов, катушки индуктивности плохо приспособлены для интегрального исполнения.

Таким образом, для применения фильтров в диапазоне низких частот из схем желательно исключить катушки индуктивности. Это достигается разработкой активных фильтров на основе резисторов, конденсаторов и одного или нескольких активных приборов, таких как транзисторы, зависимые источники и т.д. [2].

Одним из наиболее часто применяемых активных приборов является операционный усилитель.

При реализации активного фильтра разработчик должен применять те жен типы ОУ, которые отвечают предъявленным требованиям по коэффициентам усиления и частотным диапазонам. Например, коэффициент усиления ОУ с разомкнутой обратной связью должен, по крайней мере, в 50 раз превышать коэффициент усиления фильтра [2].

2. Аппроксимация фильтра

Как было показано, передаточная функция любого фильтра нижних частот может быть представлена в следующей форме:

Порядок фильтра n определяется максимально степенью P в выражении, приведенном выше, после того, как выполнено перемножение блоков второго порядка в знаменателе. Он задает асимптотический наклон амплитудно-частотной характеристики коэффициента передачи, равный – n·20 дБ на декаду. Вид частотной характеристики определяется как порядком, так и типом фильтра. Наибольшее применение находят фильтры Баттерворта, Чебышева и Бесселя, которые отличаются лишь значениями коэффициентов а_i и b_i передаточной функции. Значения соответствующих им коэффициентов для фильтров до десятого порядка и значения нормированных частот среза ʄ_gi/ʄ_g для каждого сомножителя (звена фильтра) приведены в соответствующих таблицах [2].

Амплитудно-частотная характеристика фильтра Баттерворта имеет довольно длинный горизонтальный участок и резко спадает за частотой среза. Переходная характеристика такого фильтра при ступенчатом входном сигнале имеет колебательный характер. С увеличением порядка фильтра колебания усиливаются.

Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она, однако, не монотонна, а имеет волнообразный характер с постоянной амплитудой. При заданном порядке фильтра более резкому спаду амплитудно-частотной характеристики за частотой среза соответствует большая неравномерность в полосе пропускания. Колебания переходного процесса при ступенчатом входном воздействии сильнее, чем у фильтра Баттерворта.

а)

б)

Рис. 1.2 Амплитудно-частотные характеристики фильтров четвертого (а) и десятого (б) порядков: 1 – фильтр с критическим затуханием; 2 – фильтр Бесселя; 3 – фильтр Баттерворта; 4 – фильтр Чебышева с неравномерностью 3 дБ

На рис. 1.2 показаны амплитудно-частотные характеристики четырёх рассмотренных фильтров нижних частот четвёртого и десятого порядка. Можно заметить, что характеристика фильтра Чебышева имеет наиболее крутой спад для частот входного сигнала, превышающих частоту среза, но заметную неравномерность в полосе пропускания. При увеличении равномерности амплитудной характеристики фильтр Чебышева переходит в фильтр Баттерворта [2]. Переходные характеристики этих фильтров имеют большую амплитуду колебаний при ступенчатом входном сигнале.