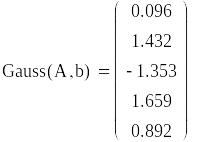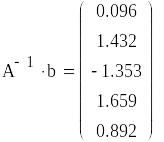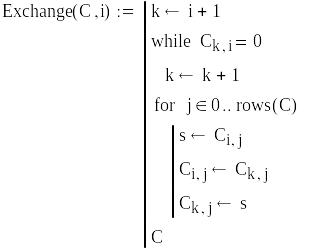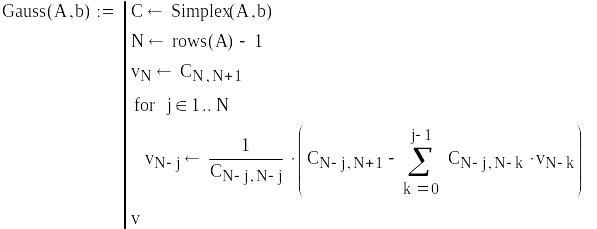Лекция № 1. Методы решения систем линейных алгебраических уравнений План
3.1. Общие сведения и основные определения
3.2. Метод Гаусса и его реализация в пакете MathCAD
3.3. Вычисление определителей
3.4. Метод простой итерации. Достаточные условия сходимости итерационного процесса
3.5. Решение систем линейных уравнений методом Зейделя
3.1. Общие сведения и основные определения
Рассмотрим систему, состоящую из m линейных алгебраических уравнений с n неизвестными:
(3.1)
которая может быть записана в матричном виде
,
(3.2)
где А прямоугольная матрица размерности mn
,
(3.3)
x вектор n-го порядка
,
b вектор m-порядка
.
Определение
3.1. Решением
системы (3.1) называется такая упорядоченная
совокупность чисел
,
,
…,
,
которая обращает все уравнения системы
(3.1) в верные равенства.
Определение 3.2. Прямыми методами решения систем линейных уравнений называются методы, дающие решение системы за конечное число арифметических операций. Если отсутствуют ошибки округления, то получаемые решения всегда являются точными.
Определение 3.3. Итерационными методами решения систем линейных называются методы, дающие решение системы уравнений как предел последовательности приближений, вычисляемых по единообразной схеме.
3.2. Метод Гаусса и его реализация в пакете MathCad
Рассмотрим систему линейных алгебраических уравнений
(3.4)
при условии, что матрица A=(aij) невырождена.
Метод Гаусса состоит в преобразовании системы (3.4) последовательным исключением переменных к равносильной системе с треугольной матрицей
(3.5)
Затем
из системы (3.5) последовательно находят
значения всех неизвестных
.
Т.о., процесс решения системы (3.4) распадается на два этапа:
1. Прямой ход приведение системы (3.4) к треугольному виду.
2. Обратный ход нахождение значений неизвестных переменных, в соответствие с (3.5).
Документ пакета MathCAD, в котором реализован метод Гаусса, состоит из следующих блоков.
1. Задание функции, анализирующую матрицу системы и переставляющую строки при обнаружении в текущей строке нулевого элемента, стоящего на главной диагонали (рис. 3.1)
2. Задание функции, приводящую матрицу системы к треугольному виду и возвращающую соответствующую расширенную матрицу системы (рис. 3.2.)
|
Рис. 3.1. Функция, переставляющая строки матрицы при обнаружении в текущей строке нулевого элемента на главной диагонали. Аргументы функции: С матрица, i номер анализируемой строки |
|
Рис. 3.2. Функция, возвращающая преобразованную к треугольному виду расширенную матрицу системы. Аргументы функции: A матрица системы, b вектор-столбец свободных членов |
3. Задание функции, возвращающей значения неизвестных, вычисленных обратным ходом в соответствие с (3.5) (рис. 3.3).
|
Рис. 3.3. Функция, возвращающая значения неизвестных, вычисленых обратным ходом в соответствие с (3.5) |
3.4. Задание матрицы системы и вектор-столбца свободных членов
3.5. Проверка правильности работы функции Simplex
3.6. Решение системы линейных уравнений методом Гаусса и проверка полученного решения средствами матричных функций пакета MathCAD
