Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«Российский государственный профессионально-педагогический университет»

Институт электроэнергетики и информатики

Кафедра общей физики

Задания и методические указания для выполнения лабораторной работы 2

по дисциплине «Физика»

для студентов всех форм обучения

направления подготовки 051000.62 Профессиональное обучение

(по отраслям)

Екатеринбург

РГППУ

2013

Задания и методические указания для выполнения лабораторной работы 2 по дисциплине «Физика». Екатеринбург, ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2013. 16 с.

Составитель: к.ф.-м.н., доцент Анахов С.В.

Одобрены на заседании кафедры общей физики ЭлИн. Протокол № 1 от 10.09.2013 г.

Заведующий кафедрой ОФ

канд.физ.-мат. наук, доцент С.В. Анахов

Рекомендованы к печати научно-методической комиссией института электроэнергетики и информатики РГППУ. Протокол №1 от 14.10. 2013 г.

Председатель научно-методической

комиссии ЭлИн А.О. Прокубовская

© ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2013

© Анахов С.В., 2013

ЛАБОРАТОРНАЯ РАБОТА 2 «ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ»

Цель лабораторной работы:

• определение ускорения свободного падения с помощью математического и физического маятников.

Задачи лабораторной работы:

• изучение процессов и параметров свободных колебаний;

• изучение параметров математического и физического маятников.

1. Теоретическая часть

Маятниковые системы начали употребляться в Европе со времен Галилео Галилея (конец ХVI – начало ХVII века) для точного измерения небольших промежутков времени путем подсчёта произведенного ими числа качаний. В эти годы Галилей опубликовал исследование колебаний маятника в котором было заявлено, что период его колебаний не зависит от амплитуды. Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Галилея привлекли внимание Христиана Гюйгенса, который изобрёл часы с маятниковым регулятором (1657), после чего появилась возможность точных измерений в экспериментальной физике (Галилей, например, при изучении законов падения считал удары собственного пульса). В 1673 году Гюйгенс опубликовал классический труд по механике «Маятниковые часы». В первых его четырёх частях Гюйгенс исследовал ряд проблем, связанных с движением маятника. В настоящее время принято рассматривать две физические модели механических маятников.

Математический маятник — осциллятор, представляющий собой механическую колебательную систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения (рис.1).

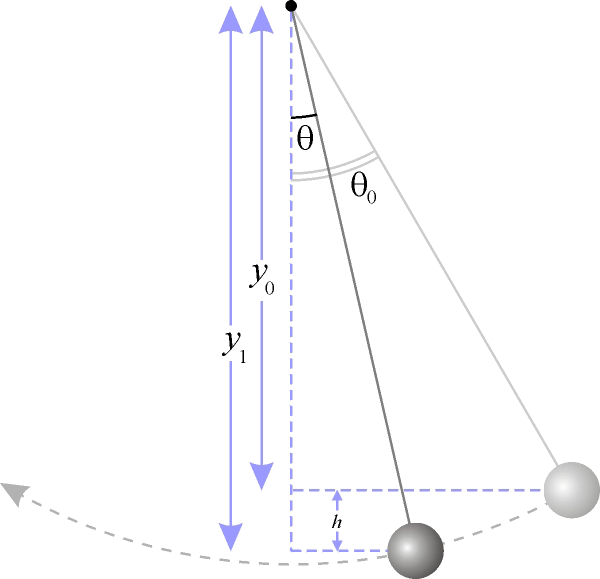
Рис.1. Математический маятник

При небольших углах отклонения (малом углеи высоте подъема h<<y₁ – рис.1) физический маятник совершает гармонические колебания. Период колебаний Т математического маятника равен:

, (1)

где 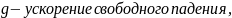l – длина нити математического маятника (расстояние от точки подвеса до центра масс шарика (l = y₁ на рис.1).

Таким образом, для определения величины с помощью математического маятника достаточно измерить его период колебаний Т и длину l, после чего рассчитать ускорение свободного падения по формуле:

, (2)

которая следует из (1).

Физический маятник– твёрдое тело, совершающее колебания относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр масс этого тела (рис.2).

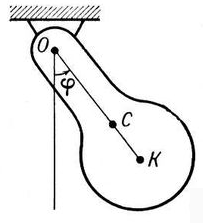
Рис.2. Физический маятник

При небольших углах отклонения (малом угле φ– рис.2) физический маятник совершает гармонические колебания, период которых определяется по формуле:

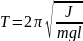, (3)

где m - масса физического маятника, l - расстояние от оси вращения 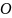до его центра масс С (l = 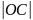на рис.2), J - момент инерции физического маятника относительно оси вращения.

Проводить измерения с помощью произвольного физического маятника, опираясь на формулу (3), достаточно затруднительно, так как при этом необходимо знать точное значение его момента инерции, положение центра масс и массу. Однако существует прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции оборотного маятника.

Оборотный маятник устроен следующим образом (рис. 3). На стержне (1) закрепляются два груза (2,3). Стержень имеет две оси вращения (4,5), расположенные по обе стороны от центра масс системы. Оси вращения для уменьшения трения выполняют в виде треугольных призм из твердого материала, которые следует устанавливать на специальную опору, закрепленную на подставке.

Рис.3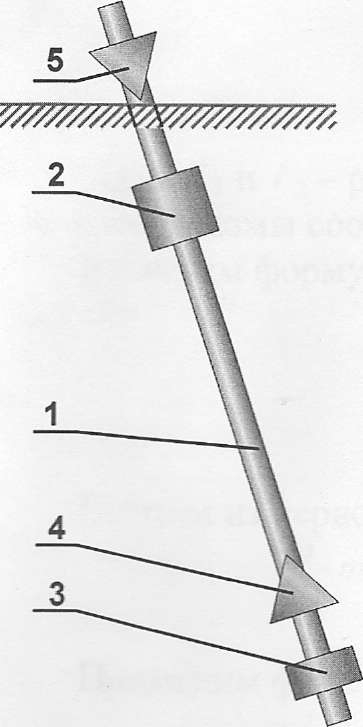

Оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка производится путем изменения взаимного расположения грузов и призм на стержне.

Выведем формулу периода колебаний оборотного маятника. Согласно формуле Гюйгенса - Штейнера. Момент инерции J маятника относительно произвольной оси вращения равен:

J = J_c+ml², (4) (4)

где J_с – момент инерции относительно оси вращения, проходящей через центр масс, m - масса маятника, а l - расстояние от оси вращения до центра масс. После подстановки (4) в (2) формула для периода колебаний физического маятника примет вид:

.

Поскольку оборотный маятник имеет равные периоды колебаний на обеих призмах (осях), полученное соотношение используем для двух расположений маятника:

(5)

Здесь l₁ и l₂ - расстояния от центра масс маятника до ребра первой и второй призмы соответственно.

Возведем формулы (5) в квадрат и умножим на знаменатели правых частей:

Вычтем из первого равенства второе и сократим на m:

,

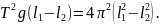
Применим формулу разности квадратов в правой части:

(6)

Если в (6) l₁ ≠l₂, что означает несимметричность расположения призм относительно центра масс маятника, то, сокращая на 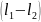, получаем:

(7)

Поскольку призмы расположены по разные стороны от центра масс, то где - расстояние между соответствующими ребрами призм (осями колебаний), или приведенная длина оборотного маятника.

На основании (7) легко записывается выражение для периода колебаний оборотного маятника:

(8)

и формула для определения g:

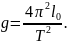(9)

Еще раз подчеркнем, что в случае (симметричное расположение осей колебаний относительно центра масс маятника), формулы (8) и (9) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от l₀ и , но и от момента инерции маятника.