3. Прямая и точка

Из инвариантного свойства 3 параллельного проецирования следует, что проекции точки К (К₁, К₂ и К₃) принадлежащие прямой а, должны принадлежать соответствующим проекциям этой прямой, т. е. если хотя бы одна проекция точки не принадлежит соответствующей проекции прямой, то эта точка не принадлежит прямой.

Из инвариантного свойства 4 следует, что проекции точки К (К₁, К₂ и К₃), принадлежащие прямой АВ, делят соответствующие проекции отрезка в том же отношении, в каком точка К делит отрезок АВ (рис. 3.2).

Рис. 3.1. Конкурирующие точки

Точки А и В, принадлежащие прямой а, и точки C, D и E, которые лежат вне этой прямой показаны на рис. 3.3.

4. Взаимные положения прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.

Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).

2. Параллельные прямые

На рис. 3.5 изображены параллельные прямые - прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

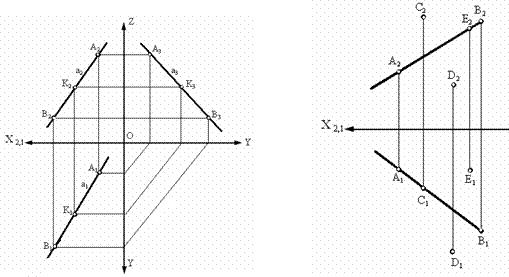
Рис. 3.2. Изображение принадлежности            Рис. 3.3. Пример принадлежности

точек А, В, К прямой а                                              точек прямой

 

Рис. 3.4. Пересекающиеся прямые

3. Скрещивающиеся прямые

Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.

На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

Рис. 3.5. Параллельные прямые                           Рис. 3.6. Скрещивающиеся прямые

 

5. Прямая и точка на плоскости

Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (∆КLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α ( (∆КLM), то пряма АВ, проходящая через эти точки, принадлежит плоскости α.

Прямые АВ и CD, принадлежащие разным плоскостям показаны на рис. 3.7. Прямая АВ принадлежит плоской фигуре LKM, потому что на проекциях прямой и плоской фигуры имеются две общих точки (рис. 3.7, а). Прямая CD принадлежит плоскости, заданной параллельными прямыми с и d, т. к. она проходит через точки С и D, расположенные на этих прямых (рис. 3.7, б).

Прямая принадлежит плоскости, если ее следы принадлежат одновременно следам плоскости.

Справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости.

Кроме того, существует еще одно свойство, определяющее взаимное положение точки и плоскости: точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой плоскости (рис. 3.7).

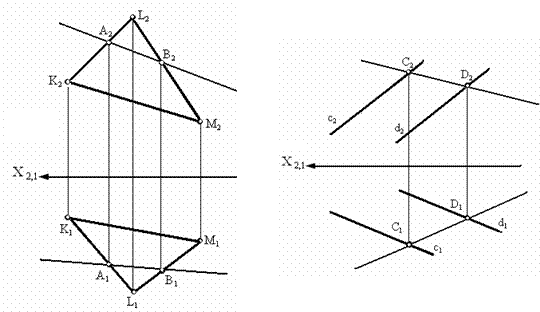
а                                                       б

Рис. 3.7. Изображение прямых, принадлежащих плоскостям