• Вопросы для самопроверки

1. Дать определение растяжению-сжатию.

2. Как строится диаграмма растяжения или сжатия?

3. Что называется пределом пропорциональности, упругости, текучести, прочности?

4. Как формулируется закон Гука?

5. Что называется удельной работой разрушения?

6. В чём разница между пластичными и хрупкими материалами?

7. Как формулируется условие прочности?

8. Что называется коэффициентом запаса прочности?

9. Какие задачи называют статически неопределимыми и каков порядок их расчета?

Тема 3. Сдвиг и кручение.

Литература: [1, гл. 4 и 6], [2, гл. 8 и 9]

Понятие о чистом сдвиге; диаграмма напряжений, закон Гука и потенциальная энергия упругой деформации при сдвиге. Связь между модулями упругости первого и второго рода и коэффициентом Пуассона. Расчёт элементов конструкций на сдвиг.

Определение кручения. Крутящие моменты и их эпюры. Напряжённое состояние при кручении круглого бруса.

Касательные напряжения в поперечном сечении и углы закручивания при кручении круглого бруса. Условия прочности и жёсткости вала.

Статически неопределимые задачи при кручении.

Понятие о кручении бруса некруглого сечения и тонкостенного стержня (открытого и замкнутого профиля).

Расчёт цилиндрических винтовых пружин малого шага.

• Указание к изучению. По закону парности касательные напряжения на двух взаимно перпендикулярных площадках равны между собой. При изучении деформаций надо обратить внимание на то, что одна из диагоналей выделенного элемента, по граням которого действуют касательные напряжения, удлиняется, а другая укорачивается. Таким образом, явление растяжения-сжатия и сдвига нельзя рассматривать изолированно друг от друга. Формула закона Гука для сдвига следующая: 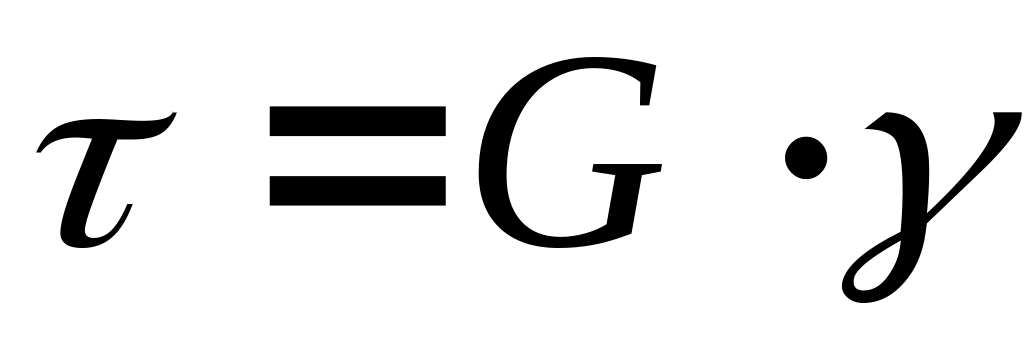. Устанавливается связь между модулем продольной упругости , модулем сдвига и коэффициентом Пуассона . Необходимо внимательно изучить вопрос о выборе допускаемых напряжений при сдвиге.

Следует обратить внимание на то, что расчеты заклёпок, сварных соединений и врубок являются условными и что явление "среза" всегда осложнено наличием других напряжений, которыми для упрощения расчётов обычно пренебрегают. Надо научится показать на чертеже площадки, на которых возникают напряжения среза, смятия, скалывания.

Рассматривается кручение бруса с прямой осью при его нагружении парами сил в плоскостях, перпендикулярных оси бруса. Дается понятие крутящего момента и вычисление его методом сечений.

При рассмотрении кручения бруса круглого, кольцеобразного, прямоугольного, тонкостенного замкнутого или тонкостенного разомкнутого поперечного сечения устанавливается связь между касательным напряжением , крутящим моментом и моментом сопротивления .

При этом для бруса круглого поперечного сечения в основу вывода зависимостей от и положена гипотеза плоских сечений, которая неприемлема для брусьев с прямоугольным поперечным сечением. В итоге получено, что касательные напряжения в поперечном сечении круглого стержня (вала) изменяются по линейному закону: от нуля на оси вала до максимального значения у его поверхности. Это значение касательного напряжения используется для условия прочности.

Для расчёта брусьев на жёсткость вводится понятие относительного и абсолютного угла поворота сечения (закручивания) и даются выражения для его определения через крутящий момент, длину бруса и жёсткость сечения.