Пример выполнения задачи 10 для рамы (схема б)

Рассмотрим расчёт рамы (рис. 28) по условию задачи 9 при , кН/м, м.

Решение

1. Определим степень статической неопределимости по формуле , где – число неизвестных связей (внутренних или внешних); 3 – число уравнений равновесия для плоской системы сил.

Подсчитаем количество реакций в раме: имеем три реакции в заделке и две в шарнирно-неподвижной опоре , всего пять. Тогда , значит, система 2 раза статически неопределима.

Выбираем основную систему таким образом, чтобы она была статически определима, но геометрически неизменяема (рис. 28, б). Из основной системы видно, что лишними неизвестными будут силы и , которые являются опорными реакциями в шарнире .

В случае, когда при выборе основной системы отбрасывается заделка, в которой возникают три усилия (момент и две силы), лишними неизвестными будут силы , и момент .

При наложении на основную систему всех внешних нагрузок и неизвестных сил и получается эквивалентная система (рис. 28, в).

Рис. 28

Рис. 28 (Окончание)

Для эквивалентной системы пронумеруем участки (их четыре) и покажем текущие координаты .

2. Так как рассматриваемая система 2 раза неопределима, то канонические уравнения метода сил имеют следующий вид:

Для вычисления коэффициентов канонических уравнений , , , , необходимо предварительно построить эпюры от внешних нагрузок и от сил и , равных единице (то есть от единичных сил).

Запишем грузовые моменты по участкам:

; ; ;

По этим значениям построим эпюру (рис. 28, г). Заметим, что для изгибающего момента принято следующее правило знаков: если наблюдатель, помещённый внутрь рамы, видит растянутые волокна стержня на каком-то участке, то на этом участке изгибающий момент положительный; если он видит сжатые волокна стержня, то изгибающий момент отрицателен.

Найдём моменты от единичных сил и :

; ;

;

По этим значениям построены эпюры единичных моментов (рис. 28, д, е).

Коэффициенты канонического уравнения находим способом Верещагина: для единичных коэффициентов , , перемножаем эпюры единичных моментов по формуле ; для грузовых коэффициентов перемножаем эпюры единичных и грузовых моментов , по формуле .

;

;

;

;

.

Подставим найденные коэффициенты в канонические уравнения:

;

.

Упростим уравнения:

Умножим первое уравнение на 3, второе на (–2):

Сложив уравнения, определим : кН.

Далее из первого найдём :

кН.

3. Построение эпюр внутренних силовых факторов производят, используя полученные значения и и внешнюю нагрузку для вычисления суммарных поперечных сил, продольной сил и изгибающих моментов (рис. 28, в). Правило знаков для поперечных сил и изгибающих моментов такое же, как для простого изгиба (смотри задачу 7), для растягивающей продольной силы ставим знак "плюс", для сжимающей – знак "минус".

I участок. :

кН; кН;

,

при ,

при кНм.

II участок. :

кН; кН;

,

при кН×м,

при кН×м.

III участок. :

кН; кН;

,

при кН×м,

при кН×м.

IV участок :

кН; кН;

,

при кН×м,

при кН×м.

Эпюры изображены на рисунке 28, ж, з, и.

Правила контроля построения эпюр и в рамных конструкциях те же, что и для балок (смотри пример выполнения задачи 7). Согласно этим правилам:

• В рассматриваемом примере в сечении, где приложена сосредоточенная сила кН (рис. 28, а), на эпюре (рис. 28, ж) наблюдают скачок на величину этой сил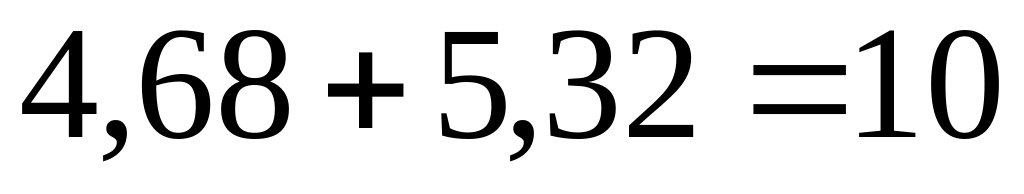ы , а на эпюре (рис. 28, и) – излом в направлении, обратном действию этой силы.

• В сечении, где приложен сосредоточенный момент кН×м (рис. 28, а), на эпюре (рис. 28, и) наблюдается скачок на величину этого момента: 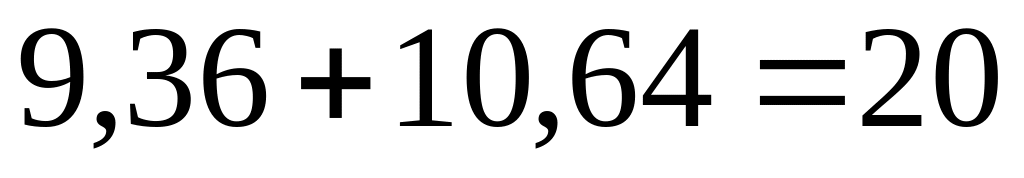кН×м.

4. Сечение рамы подбирают из условия прочности по нормальным напряжениям изгиба

,

где – максимальный изгибающий момент, взятый из эпюры суммарных изгибающих моментов, в нашем примере кН×м; – осевой момент сопротивления, для круглого сечения .

Тогда требуемый диаметр сечения

м.

Принимаем диаметр м см.

5. Перемещение по направлению (рис. 28, а) можно определить методом Верещагина, умножив эпюру моментов от вертикальной силы, равной единице (рис. 28, к), на эпюру суммарных моментов (рис. 28, и) по формуле

,

где м⁴, , , , – значения на грузовой и единичной эпюрах (рис. 28, и, к) начале и в конце каждого участка соответственно.

Используя эту формулу, получим:

см.

Положительный знак говорит о том, что перемещение происходит по направлению единичной силы, значит, вниз.