Задача 9

Ведущий шкив , вращаясь со скоростью , передаёт с помощью силы мощность на второй (ведомый) шкив, на котором в итоге возникают усилия и . (рис. 22 и 23). При этом вал подвергается кручению с изгибом.

Для вала требуется:

1. Определить крутящий момент на ведущем шкиве и построить эпюру крутящих моментов строго под схемой вала.

2. Найти окружные усилия , и на ведущем и ведомом шкивах.

Рис. 22

Рис. 23

3. Построить эпюры изгибающих моментов в двух взаимно перпендикулярных плоскостях и .

4. Построить эпюру суммарных изгибающих моментов .

5. Используя теорию наибольших касательных напряжений (III теорию прочности), подобрать диаметр вала и принять его значение, округлив до стандартных значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм.

Допускаемое напряжение для материала вала принять МПа.

Значения мощности , скорости вращения и размеры вала принять по табл. 10.

Таблица 10

Схема	, кВт	, об/мин	, м	, м	, м	, м	, м
I	30	100	0,30	0,60	0,40	0,30	0,30
II	50	200	0,40	0,70	0,55	0,40	0,35
III	35	120	0,45	0,55	0,60	0,35	0,35
IV	40	200	0,80	0,30	0,45	0,45	0,30
V	55	300	0,50	0,65	0,40	0,25	0,40
VI	60	400	0,60	0,45	0,30	0,70	0,20
VII	70	500	0,70	0,40	0,25	0,45	0,20
VIII	80	650	0,80	0,50	0,50	0,50	0,20
IX	90	300	0,90	0,55	0,20	0,30	0,30
X	85	450	0,65	0,35	0,35	0,50	0,25
е	е	д	г	д	е	г	д

Пример выполнения задачи 9

Согласно условию задачи 9 выполнить расчёт вала при кВт, об/мин, см, см, м, м, (рис. 24).

Решение

1. Определим крутящий момент, возникающий при передаче мощности, по формуле:

кНм.

Этот момент через вал передаётся на второй (ведомый) шкив, значит, на валу между шкивами имеем постоянный крутящий момент , поэтому на эпюре (рис. 24, а) будет прямоугольник, высота которого кНм.

2. Найдём окружные усилия.

Рассмотрим 1-й шкив. Крутящий момент, возникающий в сечении вала, где находится шкив , можно записать через силу как .

Отсюда окружное усилие кН.

Рис. 24

Рассмотрим 2-й шкив. Крутящий момент, возникающий в сечении вала, где находится ведомый шкив, можно записать через силы и в виде

.

Отсюда окружное усилие

кН

и усилие

кН.

3. Вал изгибается в двух взаимно перпендикулярных плоскостях, поэтому необходимо найти изгибающие моменты, действующие в двух плоскостях (в вертикальной и горизонтальной).

Для построения эпюры изгибающих моментов в вертикальной плоскости (рис. 24, б) определим реакции и из условий равновесия.

; ;

; ;

Из этих уравнений получаем кН,

.

Используя уравнение равновесия , проверим правильность найденных реакций.

: , .

Наибольший изгибающий момент возникает под силой :

кНм.

Вычислим изгибающие моменты в характерных сечениях 2 и 3 (посередине расстояния а), они будут нужны для эпюры суммарных моментов.

кНм,

кНм.

Заметим, что на опорах и для данной схемы балки изгибающий момент равен нулю.

По найденным значениям моментов построена эпюра изгибающих моментов в вертикальной плоскости (эпюра на рис. 24, б).

Аналогично построим эпюру изгибающих моментов в горизонтальной плоскости (эпюру ). Сначала вычислим опорные реакции и .

: ,

: .

Отсюда кН,

кН.

Проверим правильность найденных реакций по уравнению :

, .

Подсчитаем изгибающие моменты . Под силой будет максимальный изгибающий момент

кНм.

Момент в сечениях 1 и 3 соответственно:

кНм,

кНм.

По найденным значениям моментов построена эпюра изгибающих моментов в горизонтальной плоскости (эпюра на рис. 24, в).

4. Валы, как правило, имеют круглые поперечные сечения, у которых все оси являются главными. Чаще всего валы изгибаются в разных плоскостях, поэтому при расчёте необходимо геометрически сложить изгибающие моменты, действующие в двух взаимно перпендикулярных плоскостях, и найти суммарный изгибающий момент, который тоже будет лежать в главной плоскости инерции бруса и, следовательно, вызовет обычный плоский изгиб:

.

Если определить суммарный момент для целого ряда точек и построить эпюру , то она окажется криволинейной.

Определим , геометрически сложив изгибающие моменты и , для трех сечений 1, 2, 3, так как в одном из них наиболее вероятно опасное сечение:

кНм,

кНм,

кНм.

По этим данным построена эпюра (рис. 24, г). Наибольший изгибающий момент будет в сечении 2, и его нужно использовать в дальнейших расчётах.

5. Условие прочности по третьей теории, учитывающей одновременно изгиб и кручение, имеет вид

,

где – наибольший эквивалентный (или расчётный) момент,

кНм;

– осевой момент сопротивления, для круглого сечения .

Тогда из условия прочности найдём требуемый диаметр

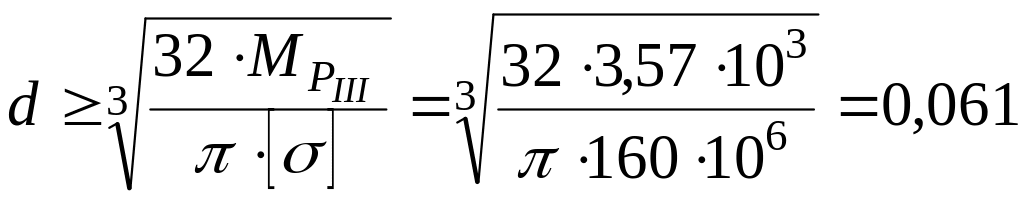м мм.

Принимаем ближайшее стандартное значение диаметра вала мм.