Представление булевой функции в виде многочлена Жегалкина, используя днф и формы логики

1. Разбиваем ДНФ на пары конъюнкций, если число слагаемых нечетно, то одно слагаемое остается без пары

2. Заменяем дизъюнкцию каждой пары конъюнкций

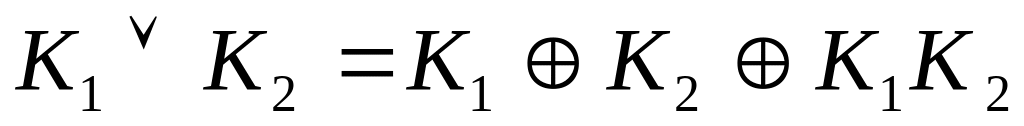
3. В полученной формуле полученные дизъюнкции заменяем 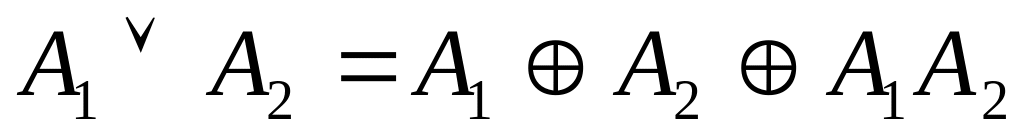и повторяем шаг, сколько возможно.

4. Заменяем инверсии

5. Раскрываем скобки

6. Вычеркиваем из полинома одинаковые слагаемые и получаем полином

Пример 1.

Пример 2. Записать функцию

в формуле полинома (многочлена) и упростить.

Решение

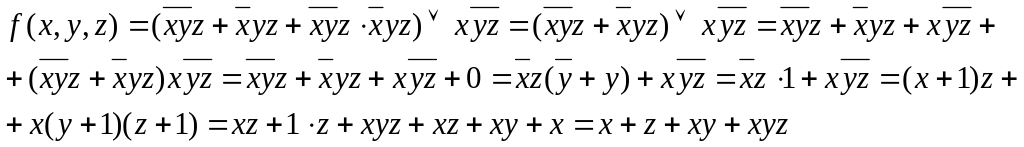
Пример 4.

Все остальные булевы функции можно представим аналогично

Представление булевой функции в виде многочлена Жегалкина, используя сднф и формы логики

Т.к. 0×1=0, то если в эквивалентности jÚy=j+y+j ×y формулы j и y являются различными константами единицы, то j ×y=0 и тогда jÚy=j+y. Следовательно, для получения полинома Жегалкина из СДНФ можно сразу заменить Ú на +.

Пример 3.

Примечание

Переменные x_i часто называют термами, полные набор из n термов образуют конституенту (константу).

Неполной дизъюнкт или конъюнкт называют импликантой.

Таким образом, полином Жегалкина можно построить следующими способами:

1. Используя формулы алгебры логики.

2. Используя ДНФ или СДНФ (при этом слагаемые, которые встречаются четное количество раз, взаимно уничтожаются).

3. Используя треугольник Паскаля, в котором используются правила сложения суммы по модулю 2 (модификация метода неопределенных коэффициентов).

4. Имеются также метод Паскаля, карты Карно и другие

Пример 4. Построить полином Жегалкина для функции с помощью СДНФ и треугольника Паскаля

х	у	х®у
0	0	1
0	1	1
1	0	0
1	1	1

Способ 1. Построим полином Жегалкина, используя СДНФ.

СДНФ – совершенная дизъюнктивная нормальная форма

1. Выделим константы 1 2. Построим для них полные конъюнкты 3. Объединим их знаком дизъюнкции
4. В СДНФ заменим на , ( - сумма по модулю 2)
Примечание: Слагаемые, которые встречаются четное количество раз, взаимно уничтожаются

Способ 2. Воспользуемся таблицей истинности и треугольником Паскаля.

С помощью треугольника Паскаля найдем функцию . При этом воспользуемся правилами сложения суммы по модулю 2: 0+0=0, 0+1=1, 1+0=1, 1+1=0.

х	у	=х®у		Треугольник Паскаля
0	0	1	1	1 1 0 1 0 1 1 1 0 1
0	1	1	0
1	0	0	1
1	1	1	1

Задания для практического занятия :