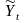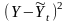Статистическое изучение динамики

Задание 35. Имеются следующие данные территориального органа Федеральной службы государственной статистики по Курганской области.

Таблица 24 – Динамика обеспеченности населения жильем

Годы	Приходится жилья на 1 чел., м2	Абсолютный прирост, м2		Темп роста, %			Темп прироста, %			Цепное абсолютное значение 1% прироста, м2
		базисный	цепной		базисный	цепной		базисный	цепной
2009	21,2
2010	21,5
2011	22,1
2012	22,5
2013	23,0

Определите абсолютные и относительные показатели ряда динамики и отразите их в таблице. Рассчитайте средние показатели ряда динамики. Сделайте выводы.

Решение:

Средние показатели ряда динамики:

• Средний абсолютный уровень ряда:

• Средний абсолютный прирост:

• Средний темп роста:

=

• Средний темп прироста:

=

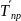Вывод:

Задание 36. Имеются следующие данные Федеральной службы государственной статистики РФ.

Таблица 25 – Динамика среднедушевых месячных денежных доходов населения РФ

Месяц	Сумма, тыс. р.	Месяц	Сумма, тыс. р.
Январь	17,6	Июль	25,7
Февраль	23,1	Август	25,8
Март	24,5	Сентябрь	24,8
Апрель	26,0	Октябрь	25,9
Май	22,8	Ноябрь	26,9
Июнь	26,2	Декабрь	38,7

Используя метод укрупнения интервалов, определите основную тенденцию развития явления.

Решение:

Таблица 26 – Динамика среднедушевых месячных денежных доходов населения РФ

Квартал	Сумма, тыс. р.
1
2
3
4

Вывод:

Задание 37. Имеются следующие данные Федеральной службы государственной статистики РФ.

Таблица 27 – Динамика оборота розничной торговли в РФ

Месяц	Сумма, млрд. р.	Месяц	Сумма, млрд.р.
Январь	1711	Июль	1991
Февраль	1690	Август	2041
Март	1840	Сентябрь	2020
Апрель	1850	Октябрь	2083
Май	1902	Ноябрь	2099
Июнь	1940	Декабрь	2517

Используя метод скользящей средней, определите основную тенденцию развития явления. Изобразите ряды динамики графически. В чем основной недостаток данного метода?

Решение:

Таблица 28 – Применение метода скользящей средней

Месяц	Оборот, млрд. р.	Скользящая средняя
		по сумме трех уровней ряда	по сумме пяти уровней ряда
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь

Рисунок 4 – Динамика оборота розничной торговли в РФ, млрд. р.

Вывод:

Задание 38. Имеются следующие данные Министерства РФ по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий.

Таблица 29 – Динамика числа чрезвычайных ситуаций в РФ

Годы	Количество чрезвычайных ситуаций, ед.
2009	429
2010	360
2011	297
2012	438
2013	335

Проведите аналитическое выравнивание количества чрезвычайных ситуаций по уравнениям прямой и параболы. Спрогнозируйте количество чрезвычайных ситуаций на 2015 г. с вероятностью 0,954. Какое уравнение наиболее точно отражает существующую тенденцию развития явления? Сделайте выводы.

Решение:

1. Аналитическое выравнивание количества чрезвычайных ситуаций по уравнению прямой.

Таблица 30 – Расчетные данные для определения параметров уравнения прямой

Годы	Количество чрезвычайных ситуаций, ед. Y	Порядковый номер года t	Расчетные значения
			t2	Yt
2009	429
2010	360
2011	297
2012	438
2013	335
Итого

• Решение системы уравнений:

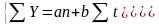
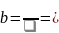
• Уравнение прямой:

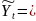
• Точечные прогноз количества чрезвычайных ситуаций на 2015 г.:

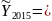
• Остаточное среднеквадратическое отклонение:

=

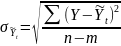• Интервальный прогноз количества чрезвычайных ситуаций на 2015 г.:

Вывод:

2. Аналитическое выравнивание количества чрезвычайных ситуаций по уравнению параболы.

Таблица 31 – Расчетные данные для определения параметров уравнения параболы

Годы	Количество чрезвычайных ситуаций, ед. Y	Порядковый номер года t	Расчетные значения
			t2	t4	Yt	Yt2
2009	429
2010	360
2011	297
2012	438
2013	335
Итого

• Решение системы уравнений:

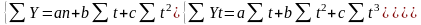
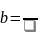
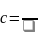
• Уравнение параболы:

• Точечные прогноз количества чрезвычайных ситуаций на 2015 г.:

• Остаточное среднеквадратическое отклонение:

=

• Интервальный прогноз количества чрезвычайных ситуаций на 2015 г.:

Вывод:

Задание 39. Имеются данные о числе расторгнутых браков населением города.

Таблица 32 – Расчет индекса сезонности числа расторгнутых браков

Месяц	Число расторгнутых браков, ед.				Индекс сезонности, %
	2011 г.	2012 г.	2013 г.	среднемесячный уровень
Январь	195	158	144
Февраль	164	141	136
Март	153	153	146
Апрель	136	140	132
Май	136	136	136
Июнь	123	129	125
Июль	126	128	124
Август	121	122	119
Сентябрь	118	118	118
Октябрь	126	130	128
Ноябрь	129	131	135
Декабрь	138	141	139
Средний уровень ряда	х	х	х			х

Определите средние значения уровней ряда для каждого месяца года, общий средний уровень, индекс сезонности по каждому месяцу. Изобразите полученные индексы сезонности в виде лепестковой диаграммы. Сделайте выводы.

Решение:

Рисунок 5 – Лепестковая диаграмма сезонности числа расторгнутых браков, %

Вывод: