Лабораторная работа № 1.

” Конечные автоматы Мили и Мура ”

1. Общие положения.

На основе теории автоматов некоторая система моделируется в виде автомата, перерабатывающего дискретную информациию и меняющего свои внутренние состояния лишь в дискретные моменты времени. (см., напр., [1]).

Автомат можно представить как некоторое устройство (черный ящик), на которое передаются входные сигналы и снимаются выходные, при этом изменяются внутренние состояния.

Конечный автомат – автомат, у которого множества значений внутренних состояний, входных и выходных сигналов конечны.

Конечный автомат можно представить как математическую схему (F-схему), характеризующуюся шестью составляющими.

1. Конечный входной автомат V. Входные сигналы v[t] в любой момент времени принимают значения из этого входного алфавита: .

2. Конечный внутренний алфавит Х. Состояние автомата x[t] принимает значения из этого внутреннего алфавита: .

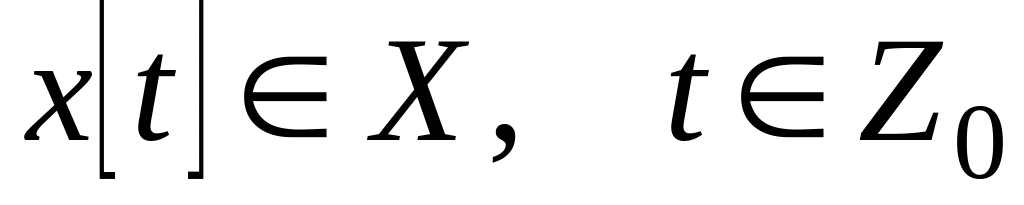3. Конечный входной алфавит Y: .

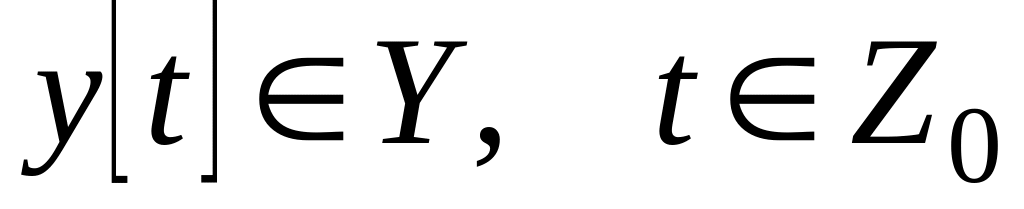4. Начальное состояние (состояние в начальный момент времени): .

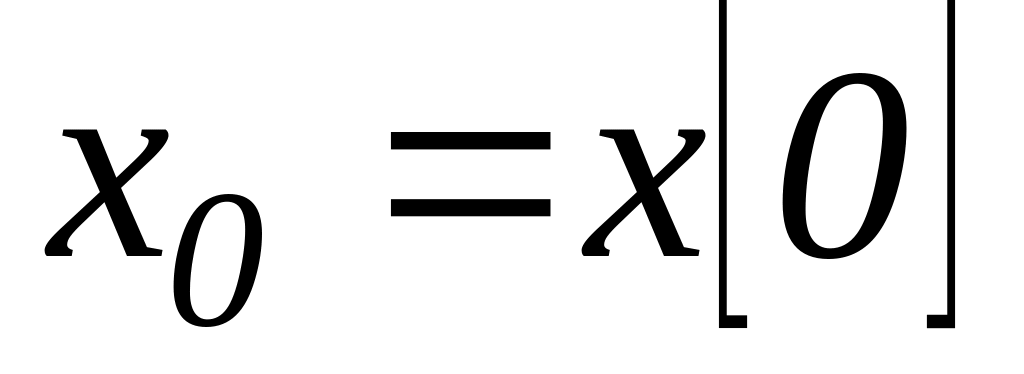5. Функция переходов позволяет определить, в каком состоянии x[t] окажется конечный автомат в некоторый момент времени t, если в предшествующий момент он был в состоянии x[t-1], а на вход поступил сигнал: .

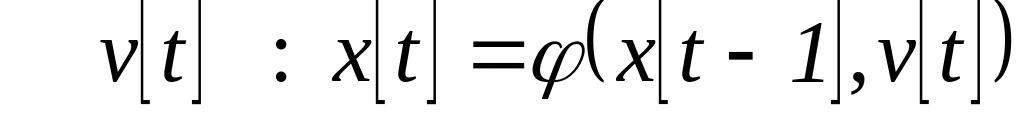6. Функция выходов определяется типом конечного автомата:

1. Для автомата Мили выход определяется состоянием автомата в предыдущий момент времени и сигналом, поступающим на вход в данный момент: .

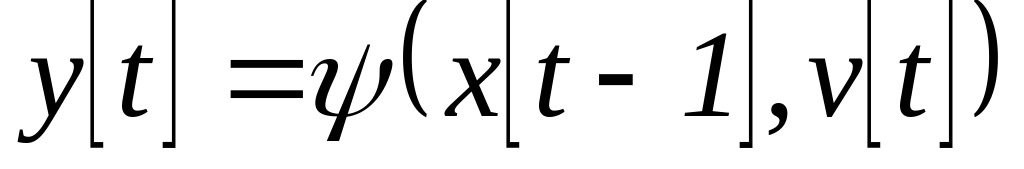2. Для автомата Мура выход определяется состоянием автомата в тот же момент времени и не зависит от входного сигнала:

Автомат, задаваемый F- схемой: , функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.

Работа конечного автомата (КА).

В каждый момент t=0, 1, 2, …дискретного времени КА находится в определенном состоянии x[t] и способен воспринимать на входном канале сигнал v[t], на который он реагирует переходом в [t+1]-м такте в новое состояние x[t+1] и выдачей некоторого выходного сигнала y[t+1] на выходном сигнале.

В общем случае конечный автомат имеет несколько входов, состояний и выходов:

Вектор, составленный из скалярных входов:

, где m - число входов.

Аналогично:

, где n – число состояний.

, где l - число выходов.

В этом случае алфавиты представляют собой прямые произведения более простых алфавитов: , каждая координата принимает значение в своем конечном алфавите.

Аналогично: .

Функции переходов и выходов допускают развернутую запись: (функция переходов для автоматов Мили и Мура).

Функция выходов для автомата Мили: .

Функция выходов для автомата Мура: .

Алфавиты входов, состояний и выходов могут иметь различную значность.

- составляющие алфавитов входов;

, J_i –значность алфавита i-го входа;

- номера входов.

- составляющие алфавитов состояний;

, J_k – значность алфавита k-го состояния;

- номера состояний.

- составляющие алфавитов выходов;

, J_p – значность алфавита p-го выхода;

- номера выходов.

Таким образом:

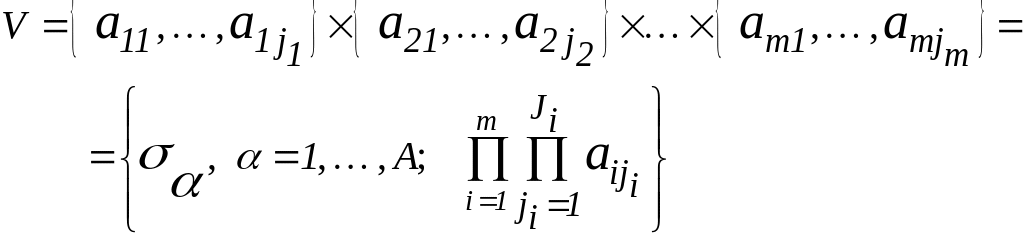
- вариант сочетания алфавитов входов v[t];

-- вариант сочетания алфавитов состояний x[t];

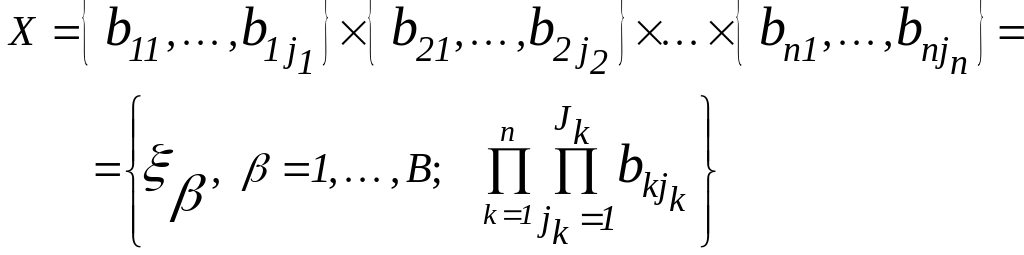
-- вариант сочетания алфавитов выходов y[t];

Конечный автомат Мура и Мили можно записать:

.

Штрих означает предшествующий момент времени.