Мультиколлинеарность

Мультиколлинеарность  это линейная взаимосвязь двух или нескольких объясняющих переменных. Последствиями мультиколлинеарности являются

1. большие стандартные ошибки 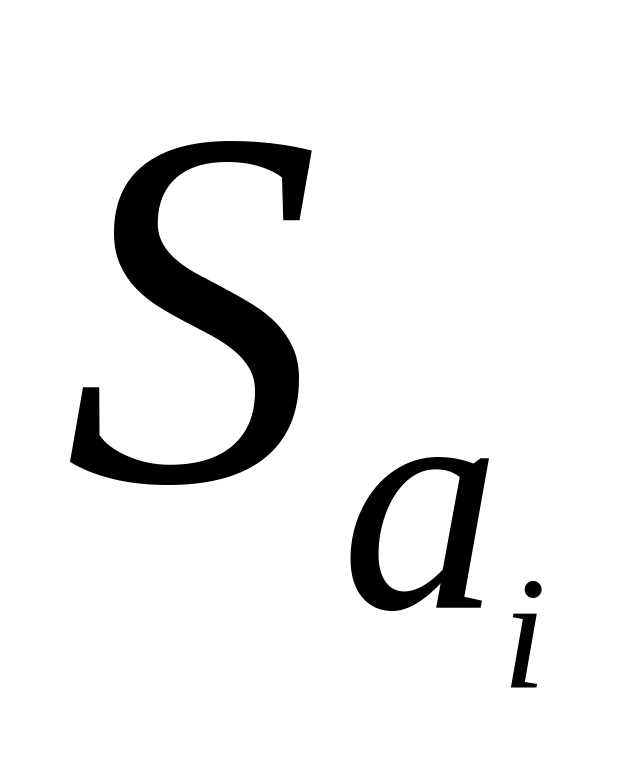, что расширяет доверительные интервалы теоретических коэффициентов уравнения линейной регрессии;

2. уменьшение статистик , что может привести к выводу о статистической незначимости коэффициента;

3. и становятся очень чувствительными к малейшим изменениям данных;

4. затрудняется определение вклада каждой из объясняющих переменных в объясняемую уравнением линейной регрессии дисперсию результативного признака;

5. возможно получение неверного знака у коэффициентов регрессии.

Точных количественных оценок для определения наличия или отсутствия мультиколлинеарности не существует. Однако есть некоторые признаки наличия мультиколлинеарности:

1. высокий коэффициент детерминации и низкие статистики некоторых переменных;

2. высокие значения частных коэффициентов корреляции (коэффициенты корреляции между двумя переменными, очищенные от влияния других переменных).

Excel позволяет вычислить корреляционную матрицу (матрицу из попарных коэффициентов корреляции) для любого количества переменных. Для этого нужно воспользоваться сервисом Сервис\Анализ данных\Корреляция. В качестве входного интервала надо указать диапазон ячеек, содержащий объясняющие переменные.

Обычно явление мультиколлинеарности считают установленным, если коэффициент парной корреляции между двумя какими-либо переменными больше 0,8.

Чтобы избавиться от мультиколлинеарности, в модель включается лишь один из линейно связанных факторов, причем тот, которых в большей степени связан с зависимой переменной.

Пример 22.

Проверить наличие мультиколлинеарности и устранить ее в случае обнаружения.

10	12	5	20
15	10	6	35
20	9	7	30
25	9	8	45
40	8	9	60
37	8	7	70
43	6	7	75
35	4	8	90
40	4	2	105
55	5	4	110

Построим регрессию с помощь соответствующего пакета.

Получаем следующие данные:

Видно, что коэффициент детерминации очень высокий, а стандартная ошибка переменной достаточно низкая. Есть подозрение на мультиколлинеарность.

Построим матрицу частных коэффициентов корреляции:

Частный коэффициент корреляции и превышает 0,8. Считаем, что имеет место мультиколлинеарность.

Для ее устранения необходимо убрать одну из переменных или .

Для этого найдем коэффициенты корреляции между , и , и выберем ту переменную, для которой этот коэффициент больше (абсолютная величина). В нашем случае в модели должна остаться переменная .

Теперь снова построим модель регрессии, без переменной . Получаем