Оценивание моделей

После того как экономическая модель сформулирована, необходимо проверить совместимость модели с реальными экономическими данными. При этом следует различать два уровня анализа: теоретический и эмпирический.

На теоретическом уровне предполагаем, что известны все возможные реализации экономических показателей (генеральная совокупность).

Зная или предполагая статистические свойства генеральной совокупности, можно теоретически определить параметры модели.

На практике множество возможных исходов неизвестно, можно наблюдать только случайно выбранные значения интересующих показателей.

На эмпирическом уровне, располагая лишь выборочными значениями экономических показателей (выборочная совокупность), можно оценить, а не определить точно значения параметров модели. Эти оценки являются случайными.

Цель оценивания — получить как можно более точно значения неизвестных параметров генеральной совокупности.

Типы зависимостей

В экономических исследованиях одной из основных задач является анализ зависимостей между переменными. Зависимость может быть строгой (функциональной) либо статистической.

Функциональная зависимость задается в виде точной формулы, в которой каждому значению одной переменной соответствует строго определенное значение другой, воздействием случайных факторов при этом пренебрегают.

В экономике функциональная зависимость между переменными проявляется редко.

Статистической зависимостью называется связь переменных, на которую накладывается воздействие случайных факторов. При этом изменение одной переменной приводит к изменению математического ожидания другой переменной.

Уравнение регрессии — это формула статистической связи между переменными. Если эта формула линейна, то имеем линейную регрессию.

Формула статистической связи двух переменных называется парной регрессией, зависимость от нескольких переменных – множественной регрессией.

Элементы математической статистики Генеральная и выборочная совокупности

Пусть необходимо исследовать некоторую совокупность объектов. Если она слишком многочисленна, либо её элементы малодоступны, либо имеются другие причины, не позволяющие изучить сразу все элементы, то из неё выбирают некоторое количество объектов для изучения. При этом первоначальное множество объектов называют генеральной совокупностью, а ряд случайно отобранных объектов – выборочной совокупностью или выборкой.

Требования, которым должна удовлетворять выборка:

1. репрезентативность, т.е. выборка должна правильно представлять генеральную совокупность (пропорции в выборки должны быть такими как в генеральной совокупности);

2. количество объектов должно быть достаточно большим;

3. выборка должна быть случайной, т.е. каждый элемент генеральной совокупности должен иметь одинаковую вероятность попасть в выборку.

Введем ряд необходимых нам понятий.

Пусть обследуется признак Х некоторой генеральной совокупности получена выборка х₁, х₂,…, х_n, где х_i – значение признака, причем эти значения могут повторяться. Пусть n_i – количество повторений признака х_i. Числа х_i называют вариантами, а числа n_i – частотами. Объёмом выборки называется количество элементов в выборке. Отсюда,

, где n – объём выборки.

Отношение называется относительной частотой выборки или частостью и обозначается p_i, т.е. .

Очевидно, что

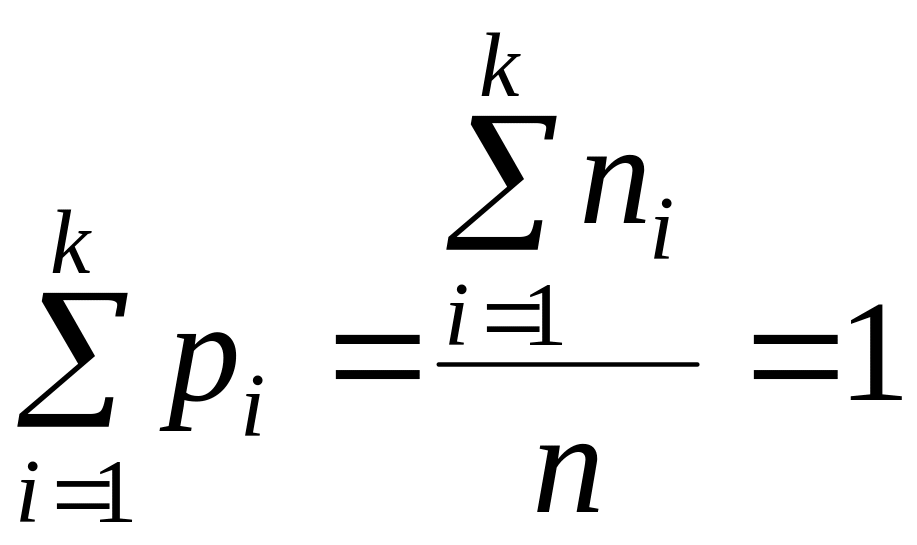
Вариационным рядом называется перечень вариантов соответствующих им частот, причем варианты располагаются в порядке возрастания. Операция по расположению значений признака в порядке их возрастания называется ранжированием.

В общем виде вариационный ряд записывается следующим образом:

Иногда вместо перечня значений x_i задают интервалы, в которые попадают элементы выборки, в качестве частоты, соответствующей интервалу принимают сумму частот вариантов, попадавших в этот интервал. Интервалы также располагают в порядке возрастания. Такой ряд называют интервальным.

В общем виде интервальный ряд записывается следующим образом:

Рекомендуется количество интервалов k выбирать по формуле Стерджеса:

.

Длина интервала определяется по формуле

.

Пример 1.

Пусть в результате исследования некоторой выборки появились следующие значения признака Х: 5, 2, 2, 16, 2, 5, 21, 21, 5, 18, 5, 21. Провести ранжирование, построить вариационный и интервальный ряды.

Решение. Сгруппируем значения признака: 2, 2, 2; 5, 5, 5, 5; 16; 18; 21, 21, 21. Вариационный ряд будет следующим:

	2	5	16	18	21
	3	4	1	1	3

Для построения интервального ряда, вычислим объем выборки n, количество интервалов k, длину одного интервала : , , .

Получаем интервальный ряд:

	[2; 6)	[6; 10)	[10; 14)	[14; 18)	[18; 22)
	7	0	0	1	4

Данные, собранные в таблицу часто трудно воспринимать, они нуждаются в наглядном представлении. Для этого используются различные формы геометрического изображения: полигон, гистограмма, кумулянта.

Полигон служит для изображения вариационного и интервального ряда и представляет собой ломаную, соединяющую точки плоскости с координатами . Для интервального ряда в качестве координат берут середины интервалов.

Гистограмма служит только для представления интервального ряда и имеет вид ступенчатой фигуры, составленной из прямоугольников с основаниями, равными длине интервалов, и высотами, равными значениям .

Кумулянта служит для изображения вариационного и интервального ряда и представляет собой ломаную, соединяющую точки с координатами , где  накопленные частоты. Для интервального ряда в качестве координат берут середины интервалов.

Пример 2.

Построить полигон, гистограмму и кумулянту по вариационному и интервальному ряду из примера 1.

Решение.

Полигон для вариационного ряда

	2	5	16	18	21
	3	4	1	1	3

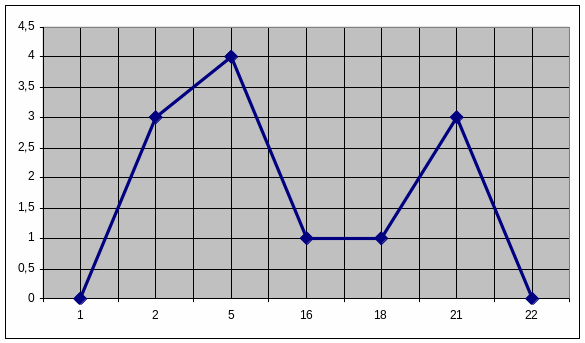
Полигон для интервального ряда

	[2; 6)	[6; 10)	[10; 14)	[14; 18)	[18; 22)
	7	0	0	1	4

Гистограмма для интервального ряда:

Кумулянта для вариационного ряда:

Кумулянта для интервального ряда: