1.Определенный интеграл. Геометрич.И экон.Смысл

О пределенный интеграл - одно из основных понятий математического анализа. Вычисление площадей, длин дуг, объёмов, работы, скорости, моментов инерции и т. д. сводится к вычислению определенного интеграла, который, в свою очередь, тесно связан с неопределенным. Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись

Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x). Экономический смысл определенного интеграла: выражает объем произведенной продукции при известной функции производительности труда.

2. Свойства определенного интеграла.

Определенный интеграл от единицы равен длине интервала интегрирования:

Постоянный множитель можно выносить за знак определенного интеграла:

Определенный интеграл от суммы функций равен сумме интегралов от этих функций:

Определенный интеграл от разности функций равен разности интегралов от этих функций:

Если верхний предел равен нижнему, то определенный интеграл равен нулю:

При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:

Пусть точка c принадлежит отрезку [a, b]. Тогда определенный интеграл от функции f(x) на отрезке [a, b] равен сумме интегралов на частичных промежутках [a, c] и [c, b]:

Определенный интеграл от неотрицательной(неположит.) функции всегда больше(меньше) или равен нулю и другие.

3. Формула Ньютона-Лейбница.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

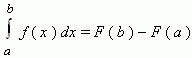
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

4. .Интегрирование подстановкой (замена переменой).

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой. При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

5. . Интегрирование по частям.

О дин из способов нахождения интеграла. Применение для нахождения опред. интеграла в целом аналогично случаю неопределённого интеграла:

Данные формулы справедливы, если каждая из функций ю и вэ непрерывно дифференцируемы на области интегрирования.