
Вариант 10 Задачи
Задача 1. Функция спроса имеет вид: QD=200-0,5P. Функция предложения имеет вид: QS=2P-50
Государство ввело субсидию на производство в размере 10 ден. ед. на единицу товара.
Определите:
А) первоначальное равновесие;
Б) равновесие после введения субсидии;
В) выигрыши потребителя и производителя после введения субсидии.
Решение:
Допустим QD= QS ;200-0,5P=2P-50→Р=100, тогда
QD = 150 QS = 150
а) на рынке установилась равновесная цена;
б) После введения субсидии на производство в размере 10 ден. ед. на единицу товара, спрос - увеличиться: QD=200-0,5*10=195
а предложение - уменьшиться: QS=2P-50=2*10-50=-30
в) Теория спроса и предложения показывает, что если спрос больше предложения – образуется избыточный спрос, ведущий к дефициту. Меняются планы продавцов, они могут наращивать выпуск товаров.
В выигрыше после введения субсидии останутся продавцы товара.
Задача 2.Потребитель тратит свой доход на приобретение товаров X и Y:
X=0,6J; Y=0,3J при PX=PY=1. Отвечают ли мотивы данного потребителя требованию функции Энгеля?
Решение:
Кривая Энгеля — график, иллюстрирующий зависимость между объёмом потребления товаров или услуг и доходом потребителя при неизменных ценах и предпочтениях. Закон Энгеля — экономический закон, согласно которому поведение потребителей связано с размером получаемого ими дохода, и по мере роста доходов потребление населением благ возрастает непропорционально. Расходы на питание возрастают в меньшей степени, чем расходы на предметы длительного пользования, путешествия или сбережения. А структура потребления продуктов питания изменяется в сторону более качественных продуктов. Рост доходов приводит к увеличению доли сбережений и потреблению высококачественных товаров и услуг, при сокращении низкокачественных.
Задача 3. Предположим, что когда фирма увеличивает применяемый капитал с 120 до 150 ед. и используемый труд с 500 до 625 ед., выпуск продукции увеличивается с 200 до 220. Какая отдача от масштаба производства имеет в данном случае?
Решение:
Отрицательный, т.к. вложения капитала происходит на 30 ед., труда на 125 ед., а выпуск продукции увеличивается всего на 20 ед.
Долгосрочный период – это период достаточно продолжительный, при котором фирма может изменить размеры своего предприятия, свои производственные мощности и количество всех задействованных ресурсов. Следовательно, все ресурсы являются переменными.
В долгосрочном периоде действует закон – «эффект масштаба», т.е. рост масштабов производства. Он бывает положительный и отрицательный.
Положительный эффект масштаба – эффект массового производства, или экономия за счет масштабов деятельности. Он объясняет нисходящую часть кривой LATC. По мере роста размеров предприятия, целый ряд факторов снижает средние издержки производства:
Специализация труда и управленческого персонала.
Более эффективное использование «капитала». Например, применение более совершенной технологии, оборудования и пр.
Производство побочных продуктов, переработка отходов.
Увеличение количества всех занятых ресурсов на 10% вызывает более чем пропорциональный прирост производства на 20%, и LATC понижаются.
Отрицательный эффект масштаба – возникает из-за сложности управления крупномасштабным производством, падает эффективность системы контроля и координации операций фирмы. Объясняет восходящую часть кривой LATC. Влияют технические и организационные факторы. Увеличение объема всех занятых ресурсов на 10% вызывает непропорциональный рост производства на 5%, и LATC повышаются.
Кривая LATC – долгосрочных средних общих издержек.

Кривая LATC - долгосрочных средних общих издержек.
Задача 4. Даны функции затрат монополии и функции спроса на двух сегментах рынка: TC=5Q+0,25Q2, Q1=160-P1, Q2=160-2P2. Найти объёмы продаж и цены на каждом из двух сегментов рынка, при которых прибыль монополии будет максимальной. Как изменится объём продаж, цены и прибыль, если ценовая дискриминация будет запрещена государством.
Решение:
Условие максимизации прибыли монополиста: MC=MR П(max)=TR-TC TC'=MC=5+0.5Q Выразим функцию спроса через цену, затем приравниваем 160-Q1=5+0.5Q, отсюда получаем Q1=103.3, P1=56.7.
Q=160-P => P=160-Q MC=5+0.5*Q TR=P*Q=(160-Q)*Q=160Q-Q^2 MR=160-2Q Приравниваем MC=MR 5+Q/2=160-2Q 5Q/2=155 5Q=310 Q=62 Подставляем в предложение P=160-Q => P=160-62=98
Аналогично для второго сегмента считаем, получается Q2=75, P2=42.5. Из теории получается, что отсутствие дискриминация государства отсутствует.
Задача 5. Фирма находится в условиях совершенной конкуренции на рынке данного товара и труда. Её производственная функция имеет вид: Q=120L -2L2 в интервале использования труда от 15 до 30 единиц. Ставка заработной платы (W) равна 60 ден. ед., а цена товара (P) – 8 ден. ед. Определить оптимальный для фирмы объём выпуска продукции.
Решение:
бщее условие максимизации прибыли при покупке фактора производства.
Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:
MRPL = MIC
где
MRPL – предельная доходность труда,
МIC – предельные издержки на фактор производства (труд).
MRPL = MR × MPL
где
MR – предельная выручка,
MPL – предельный продукт труда.
Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда.
Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае:
Р = МR
На рынке труда издержки фирмы на труд равны ставке заработной платы:
MIC = W,
где
W – ставка заработной платы
Таким образом, для совершенно конкурентной во всех отношениях фирмы условие максимизации прибыли при покупке фактора производства будет иметь вид:
P × MPL = W
Продифференцируем производственную функцию и найдём предельный продукт труда (MPL) по формуле:
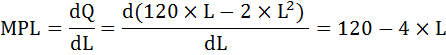
Формула предельного продукта труда
Подставим это выражение в условие максимизации прибыли и найдём количество нанимаемого труда:
8 × (120 – 4 × L) = 60
960 – 32 × L = 60
900 = 32 × L
L = 28,125
Оптимальный для фирмы выпуск продукции будет равен:
Q = 120 × 28,125 – 2 × 28,125 2 = 1793
