5. Прохождение частицы сквозь потенциальный барьер. Туннельный эффект.

Мы считали, что на границах потенциальной ямы волновая функция становится равной нулю. В действительности дело обстоит сложнее.

Движение электрона с постоянной скоростью внутри потенциальной ямы описывается плоской волной де Бройля. На границе, где проходит скачкообразное изменение потенциала, эта волна должна вести себя аналогично электромагнитной волне на границе двух сред с различными показателями преломления.

Как известно, такая волна на границе частично отражается, а частично проходит через границу. Даже в случае полного внутреннего отражения наблюдается частичное проникновение света во вторую среду. Волна де Бройля на границе потенциальной ямы также испытывает отражение, но частично проходит в область вне потенциальной ямы. Другими словами, имеется определенная вероятность обнаружить электрон за пределами потенциальной ямы.

Этот результат существенно отличается от выводов классической физики. Частицы, подчиняется законам классической физики, может выйти из потенциальной ямы при условии, что ее полная энергия превышает «глубину» потенциальной ямы. С классической точки зрения частица, находящаяся внутри потенциальной ямы «заперта» в ней. Стенки потенциальной ямы представляют для нее потенциальный барьер, который частица преодолеть не может. Для того, чтобы частица могла выйти из потенциальной ямы или проникнуть в нее, согласно классической физики ей нужно сообщить энергию, равную или большую разности высоты барьера и ее собственной энергии.

Уравнения Шредингера для стационарных состояний:

( для области 1)

(для области 2)

(для области 3)

Анализ решений для разных областей

Область 1: первое слагаемое ― плоская волна, распространяющаяся в положительном направлении оси Х (соответствует частице, движущейся в сторону барьера), а второе ― волна, распространяющаяся в противоположном направлении, то есть отраженная то барьера (соответствует частице, движущейся от барьера налево).

Область 2: в этой области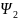 не соответствует плоским волнам (показатели экспонент действительные).

Область 3: в этой области имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо, поэтому равна нулю.

Рисунок 4

Таким образом, частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины.

Квантовая механика приводит к специфическому квантовому эффекту ― туннельному эффекту, в результате которого микрообъект может «пройти» сквозь потенциальный барьер. Для его описания водится понятие прозрачности (коэффициент прозрачности) D потенциального барьера.

Если по аналогии с оптикой для волн де Бройля посчитать интенсивность 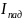падающей на барьер волны и интенсивность волны, прошедшей сквозь барьер, то, по определению, прозрачностью потенциального барьера называется величина

. (14)

Ее можно рассматривать как вероятность прохождения волн де Бройля сквозь потенциальный барьер, или, что, то же самое, как вероятность просачивания частицы, описываемой волной де Бройля, сквозь потенциальный барьер.

Формулу (14) можно преобразовать к виду, удобному для практического применения

, (15)

где ― постоянный множитель, принимаемый обычно равным единице. D сильно зависит от массы m частицы, ширины , барьера и от ; чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.