1. Постановка задачи оптимального управления. Критерии оптимальности.

Целенаправленное действие, заключающееся в получении лучших результатов и условии.

Кибернетика –наука о управлении.

Целевая функция или критерий оптимальности – математическая зависимость, которая отражает заинтересованность в работе исследуемой системы или объекта и является количественной мерой этой заинтересованности.

При правильной постановке задачи должны выполняться след-е условия:

1. нахождение оптимального значения только одного критерия;

2. наличие степеней свободы (область варьирования параметров).

Т.о., при правильной постановке задачи оптимизации формируется 1 критерий оптимальности, и указываются ограничения, выделяющие в плоскости управляющих воздействий варьируемых параметров.

2. Экономическая оценка эффективности процессов.

Наиболее общей постановкой оптимальной задачи служит выражение критерия оптимальности в виде экономической оценки. Экономический критерий оптимальности в общем случае можно записать следующим образом:

Q=Q(B,Ф,Э,К) ,

где В – производительность, Ф – объем капитальных вложений, Э – эксплуатационные затраты, К – качественный показатель.

Конкретный вид функции определяется постановкой задачи оптимизации и определяется суммой

Sпр=1/B*(Sт+Sк+Sэ)-себестоимость.

3. Постановка задачи оптимального управления в статике.

Оптимальное управление в статике характеризуется тем, что находятся значение управления, при которых целевая функция в установившемся режиме принимает max или min значение. Мат. модель есть совокупность алгебраических уравнений. Оптимальное значение есть совокупность чисел. Постановка задачи в статике звучит следующим образом: найти оптимальное управляющее воздействие из области допустимых управлений, доставляющие целевой функции max или min значение.

,

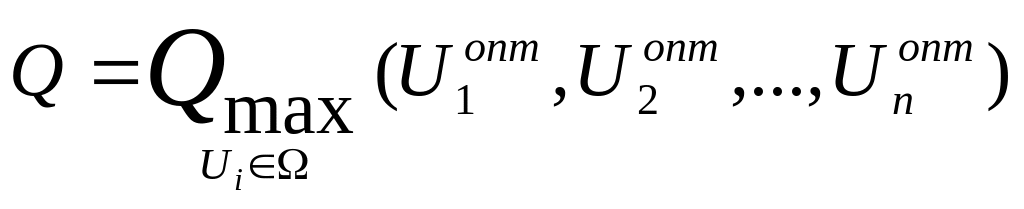4. Постановка задачи оптим-го управления в динамике.

Мат.модель такого процесса – диф.уравнение.

Изучение поведения процессов во времени.

Т.о., задача оптимального управления в динамике ставится след-м образом: задана система уравнений (*), заданы нач и конеч точки пространства от до и требуется так подобрать управления, чтобы система перешла из нач в конеч точку и при этом

критерий оптим-ти принял оптимальное значение. В этом случае критерий

оптимальности есть функционал.

5.Исследование на экстремум одномерной целевой функции методом классического анализа

Метод применяется в случаях, когда есть аналитическое выражение целевой функции, причем эта функция дифференцируема и имеет непрерывные производные. Сущность метода состоит, что целевую функцию дифференцируют по управлению и эту производную используют для записи необходимого условия.

Необходимое условие экстремума: dQ/dU=0 (*) . Из этого условия определяют точку подозреваемую на экстремум. Далее нужно определить достаточное условие существования экстремума, чтобы определить будет ли экстремум. Достаточное условие существования экстремума определяется наиболее распространенно по производной высшего порядка: если порядок производной впервые не обращающейся в ноль в т. подозреваемой на экстремум, для которой выполняется условие (*), нечетный, то в этой точке нет ни минимума, ни максимума.

Если порядок 1-ой не обращающейся в 0 пройзводной в указанной точке четный, то в данной точке есть экстремум. Причем:

минимум: d²ⁿQ\dU²ⁿ>0

максимум:d²ⁿQ\dU²ⁿ<0