6. Определение внутренних усилий, нормальных напряжений, осевых перемещений при растяжении (сжатии) в различных случаях загружения стержня. Построение эпюр
1
.5
Деформация растяжения и сжатия
Этот вид деформации показан на рис.1.5.
Δl = l1- l – абсолютная продольная деформация.
Δd = d – d1 – абсолютная поперечная деформация.
ε = Δl/l – относительная продольная деформация.
ε1 = Δd/d – относительная поперечная деформация.Очевидно, что эти две деформации взаимосвязаны. Первым эту связь установил Пуассон.
Рис. 1.5
μ = ε1/ ε = 0,25…0,33 ≈ const.
При растяжении или сжатии внутри стержня возникают только нормальные силы, а значит только нормальные напряжения. Поэтому можем записать условие прочности. σ = Ν/Α ≤ [σ] - условие прочности при растяжении (сжатии) (1.2) Между напряжением и относительной продольной деформацией существует зависимость, которую первым установил Гук. σ = Е*ε (1.3)
- напряжение пропорционально относительной продольной деформации. Здесь Е – модуль упругости первого рода или просто модуль упругости. Он характеризует жесткость материала, то есть его способность сопротивляться деформированию. Для стали Е = 2*105 МПа.
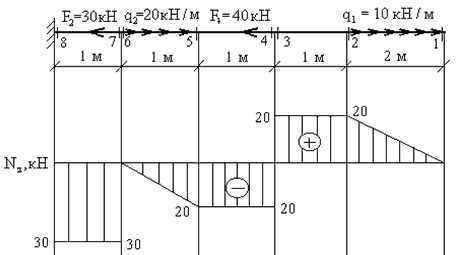
Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной - в противном случае.1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
По
найденным значениям строим эпюру Nz.
Положительные значения откладываются
(в выбранном масштабе) над осью эпюры,
отрицательные - под осью.
7.Коэффициент Пуассона. Закон Гука.
К
оэффициент Пуассона -величина
отношения относительного поперечного
сжатия к относительному продольному
растяжению. Этот коэффициент зависит
не от размеров тела, а от природы
материала, из которого изготовлен
образец.
где:
-
коэфиц Пуассона,
-
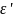деформация в поперечном направлении
(отрицательна при осевом растяжении,
положительна при осевом сжатии)
-
продольная деформация (положительна
при осевом растяжении, отрицательна
при осевом сжатии). Между напряжением
и относительной продольной деформацией
существует зависимость, которую первым
установил Гук. σ=Е*ε (1.3) - напряжение
пропорционально относительной продольной
деформации. Здесь Е – модуль упругости
первого рода или просто модуль упругости.
Он характеризует жесткость материала,
то есть его способность сопротивляться
деформированию. Для стали Е = 2*105 МПа.
Закон Гука можно записать и в другом
виде. Подставив вместо σ = Ν/Α, а вместо
ε = Δl/l, получим Δl = Ν*l/( Е*Α)
(1.4)Формула (1.4) позволяет определить
абсолютную продольную деформацию Этот
вид деформации показан на рис.1.5.
Δl = l1- l – абсолютная продольная деформация.
Δd = d – d1 – абсолютная поперечная деформация.
ε = Δl/l – относительная продольная деформация.
ε1 = Δd/d – относительная поперечная деформация.
Рис. 1.5