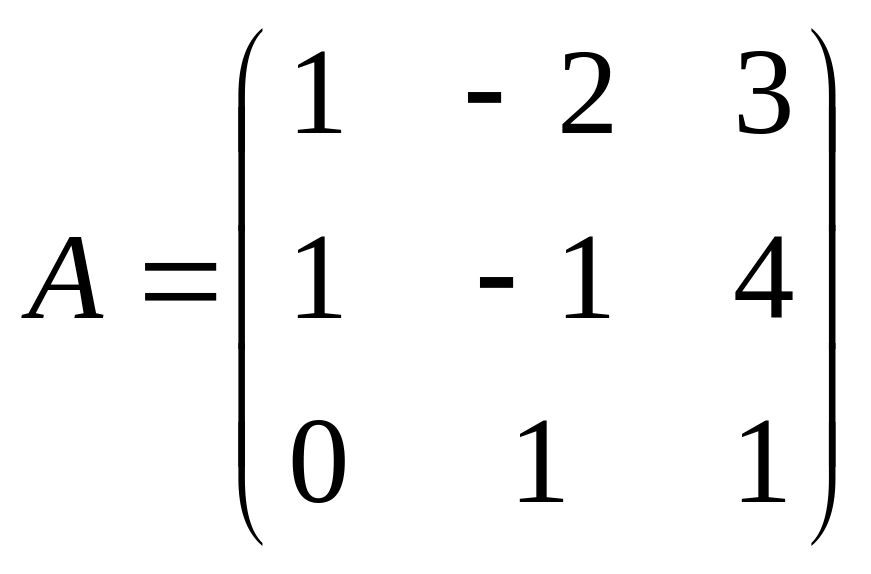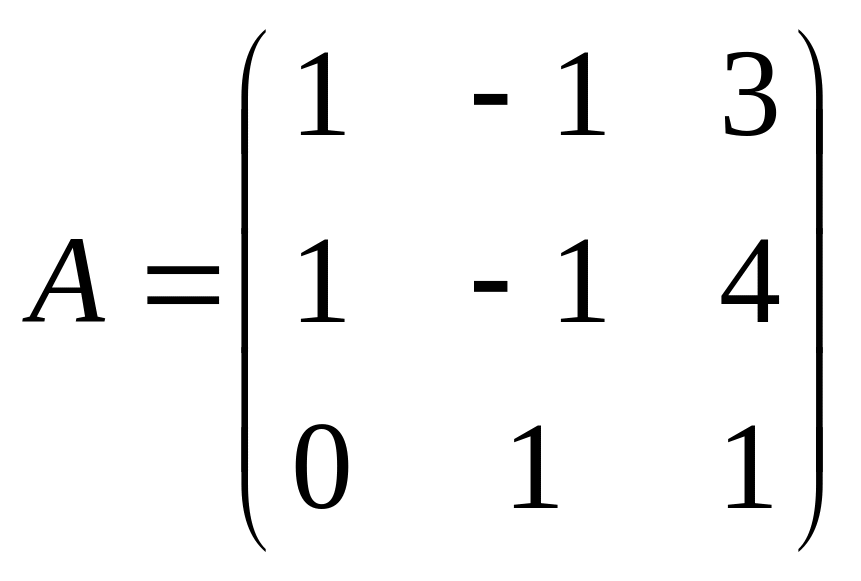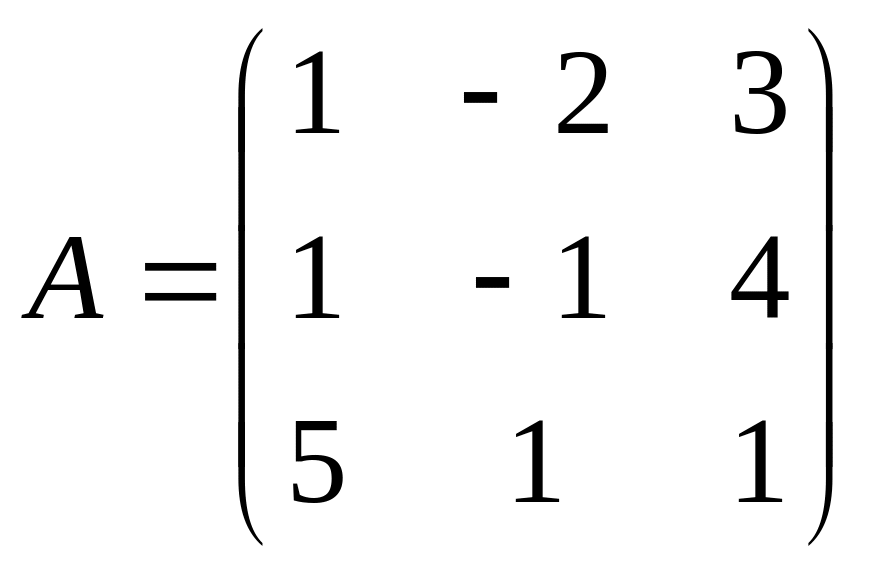Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

praktika_3_po_LA_Opredeliteli.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

422.91 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Свойства определителей.

Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен 0.

Например:

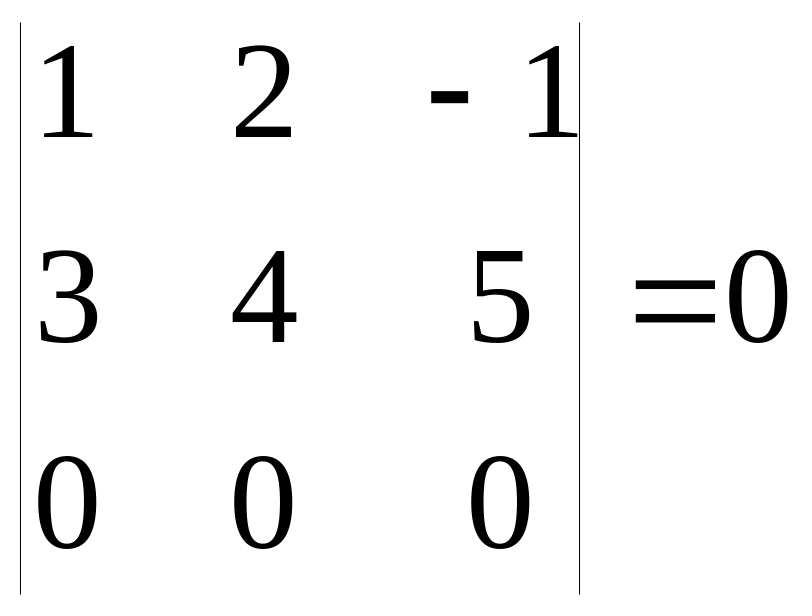
или

Если все элементы какой-либо строки (столбца) матрицы умножить на число X, то её определитель умножится на это число X.

Например:

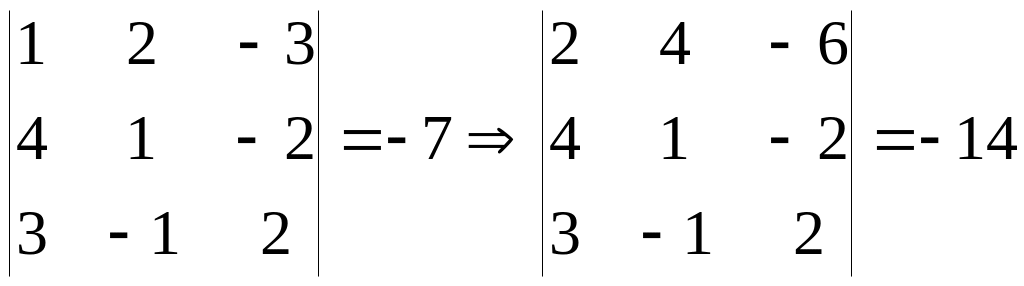
или

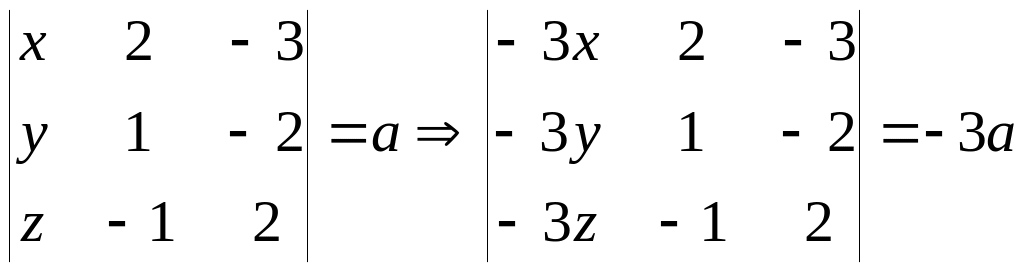
Замечание. За знак определителя можно выносить общий множитель любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех элементов.

Например:

При транспонировании матрицы её определитель не изменяется: |А'|=|А|.

Например:

При перестановке двух строк (столбцов) матрицы её определитель меняет знак на противоположный.

Например:

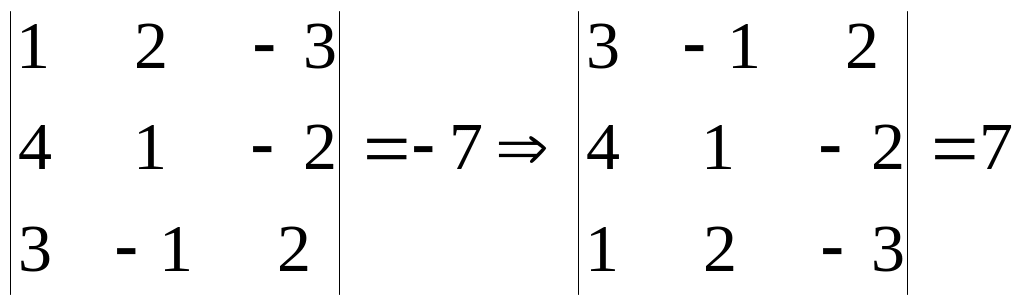
или

Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

Например:

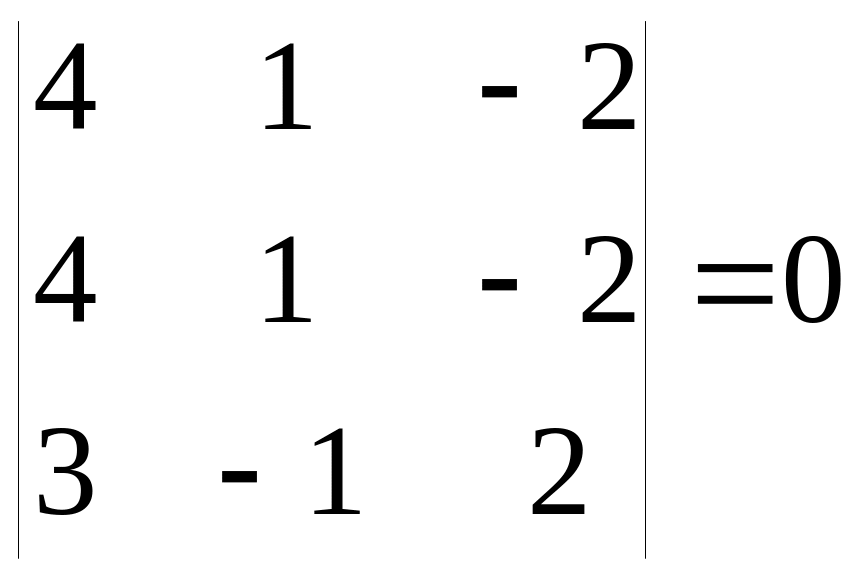
или

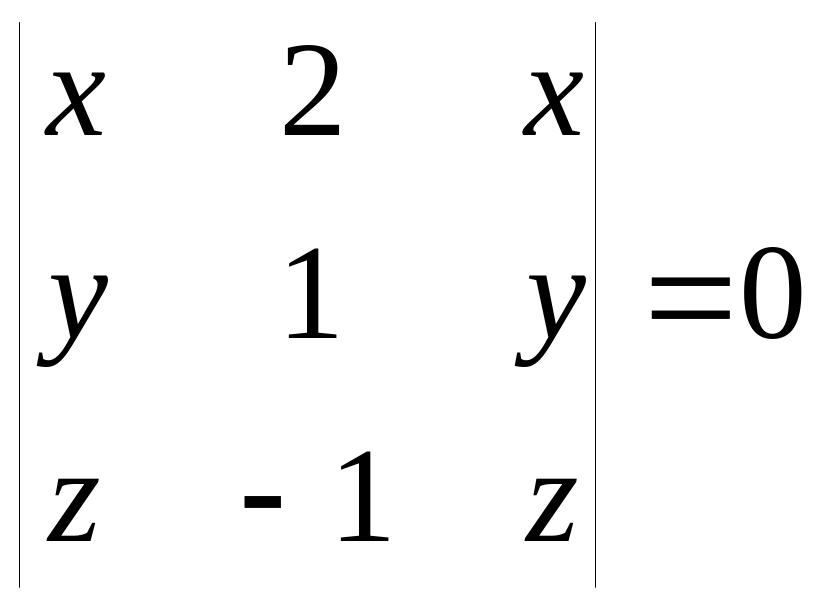
Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель равен 0.

Например:

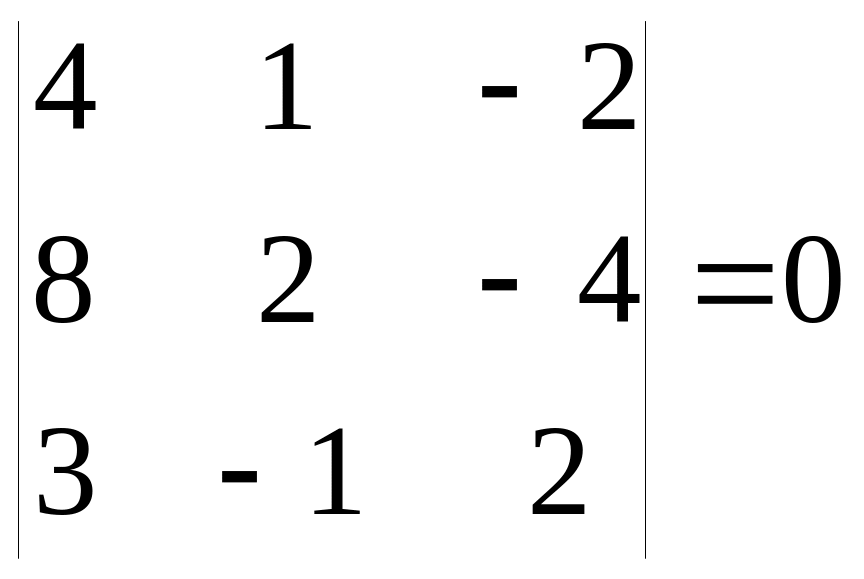
или

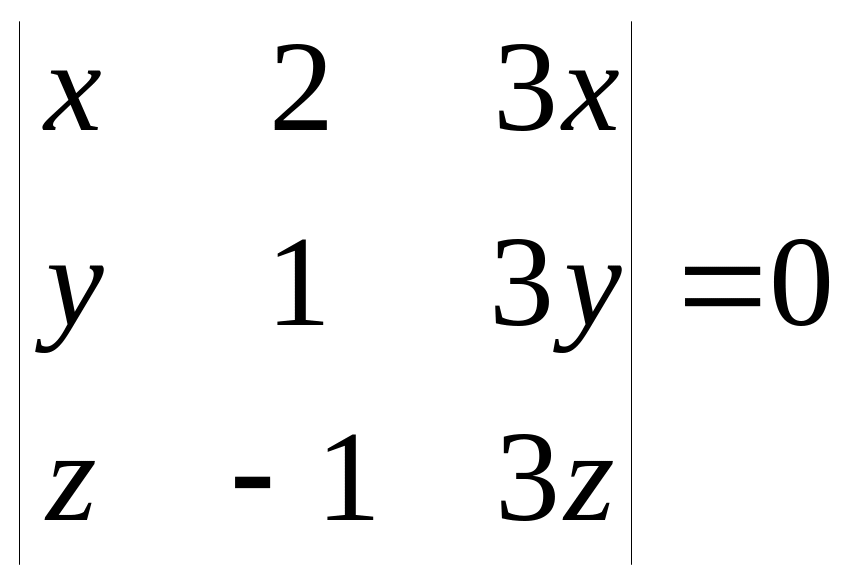
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0 (напоминаем, что сумма произведений элементов какой-либо строки (столбца) на свои алгебраические дополнения равна определителю).

Например:

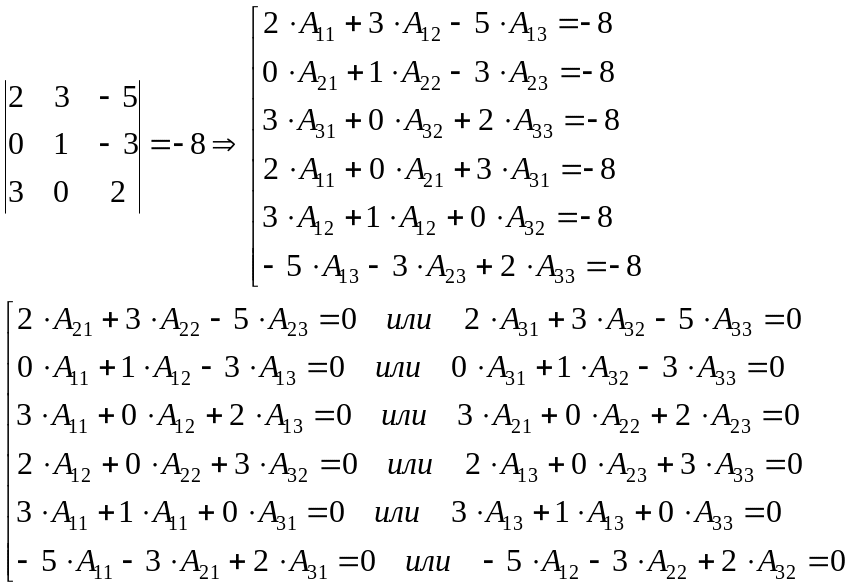
Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Например:

или

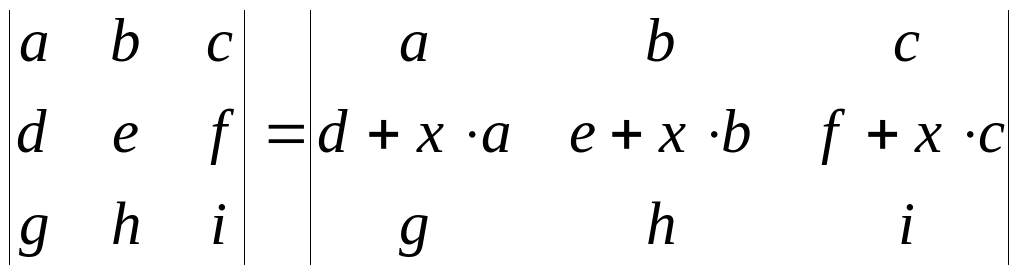
Сумма произведений произвольных чисел b₁, b₂, …, b_n на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа b₁, b₂, …, b_n.

Например:

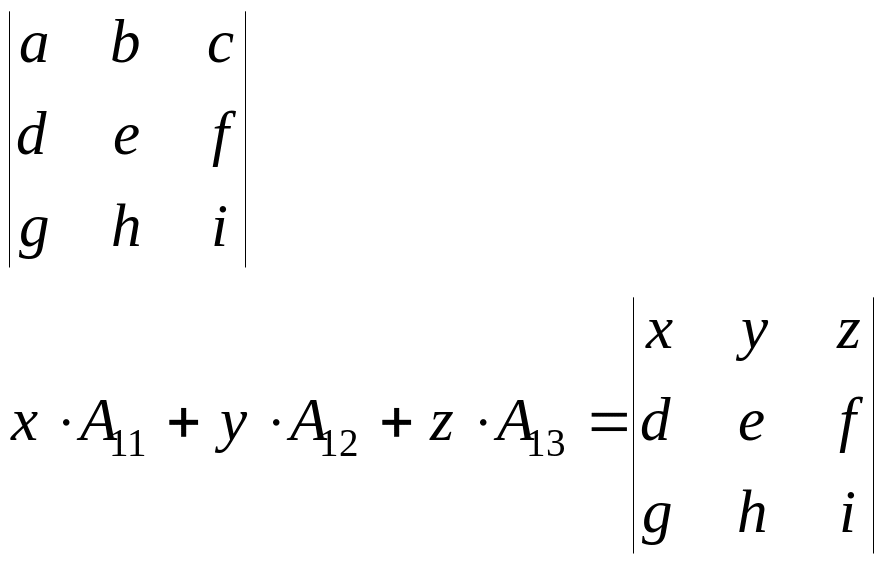
Свойство вытекает непосредственно из теоремы Лапласа.

Определитель произведения двух квадратных матриц равен произведению их определителей: |С|=|A|·|B|, где С=А·В; А и В — матрицы n-го порядка.

Например:

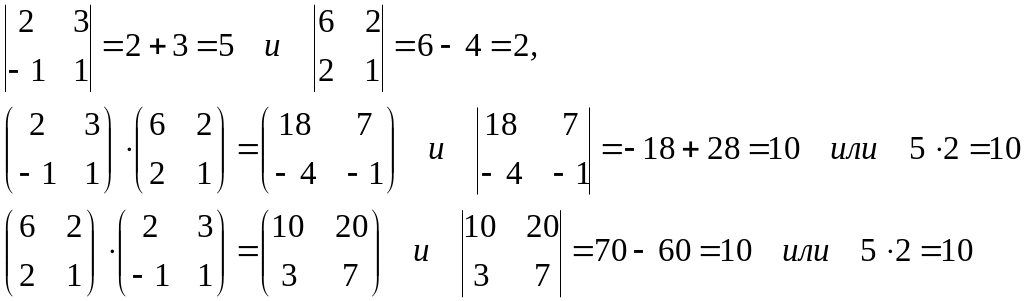
Замечание. Из свойства 10 следует, что даже если АВВА, то |АВ|=|ВА|.

Если каждый элемент какой-либо строки (столбца) матрицы представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, с соответствующими слагаемыми в рассматриваемой строке (столбце).

Например:

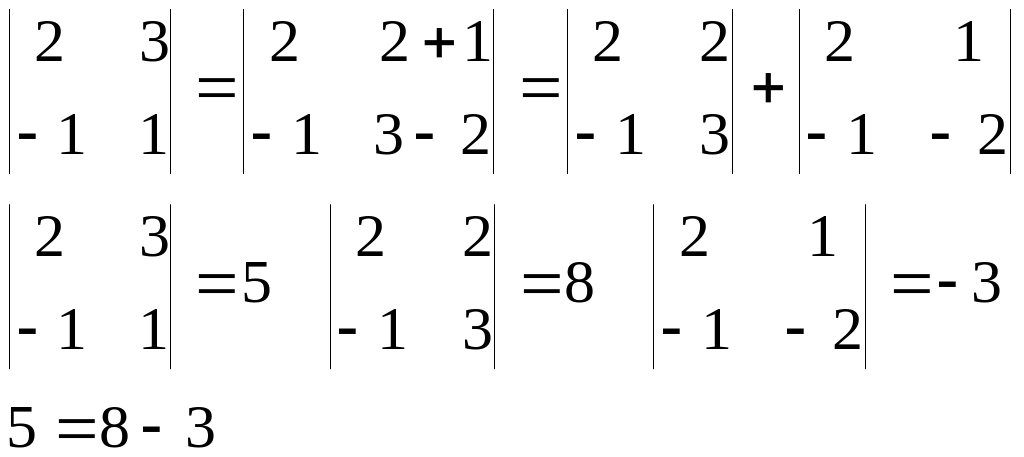
или

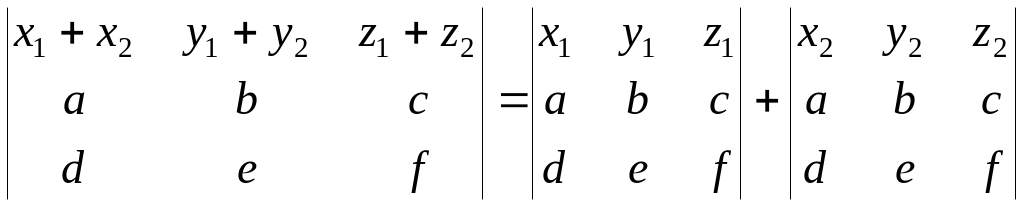
Определители. Теория.

Указать матрицы, для которых можно вычислить определитель

Указать формулу для вычисления определителя матрицы второго порядка
а₁₁· а₂₂- а₁₂· а₂₁	а₁₁· а₂₂+а₁₂· а₂₁	а₁₁· а₁₂- а₂₁· а₂₂	а₁₂· а₂₁- а₁₁· а₂₂
Записать минор элемента а₁₂ матрицы

Записать алгебраическое дополнение элемента а₁₂ матрицы

Записать минор элемента а₃₁ матрицы

Записать алгебраическое дополнение элемента а₃₁ матрицы

Вычислить минор и алгебраическое дополнение элемента а₃₂ матрицы
-1; -1	1; -1	-1; 1	1; 1
Вычислить минор и алгебраическое дополнение элемента а₂₂ матрицы
-14; -14	14; -14	-14; 14	14; 14
Укажите правильное утверждение:
все алгебраические дополнения некоторой матрицы, могут быть равны соответствующим минорам	определитель второго порядка может принимать значение, большее, чем определитель четвёртого порядка	можно вычислить миноры к элементам неквадратной матрицы	у матрицы размера тп всего тп алгебраических дополнений
Укажите правильное утверждение:
определители квадратных транспонированных матриц равны между собой	при умножении всех элементов квадратной матрицы на любое число , её определитель также умножится на 	при умножении всех элементов матрицы второго порядка на любое число , её определитель умножится на ²	если определитель имеет строку равную столбцу, то он равен нулю
Укажите правильное утверждение: для квадратной матрицы А выполняется: если \|A\|=x, то
\|-A\|=x	\|-A\|=-x	или \|-A\|=x, или \|-A\|=-x	\|-A\|=0
Укажите правильное утверждение: для матрицы А второго порядка выполняется: если \|A\|=x, то
\|-A\|=x	\|-A\|=-x	или \|-A\|=x, или \|-A\|=-x	\|-A\|=0
Укажите правильное утверждение: для матрицы А третьего порядка выполняется: если \|A\|=x, то
\|-A\|=x	\|-A\|=-x	или \|-A\|=x, или \|-A\|=-x	\|-A\|=0
Укажите правильное утверждение: для квадратной матрицы А выполняется: если \|A\|=x, то
\|A²\|=x	\|A²\|=0	\|A²\|=x²	\|A²\|=-x
Укажите правильное утверждение: для квадратных матриц А и В: если \|A\|=x и \|В\|=у, то
\|A+В\|=x+у – выполняется для всех матриц; \|A·В\|=x·у– выполняется для всех матриц;	\|A+В\|=x+у – выполняется не для всех матриц; \|A·В\|=x·у– выполняется для всех матриц;	\|A+В\|=x+у – выполняется для всех матриц; \|A·В\|=x·у– выполняется не для всех матриц;	\|A+В\|=x+у – выполняется не для всех матриц; \|A·В\|=x·у– выполняется не для всех матриц;
Укажите правильное утверждение:
при перестановке двух строк или столбцов определитель меняет знак;	величина определителя не изменится, если столбцы поменять местами;	величина определителя не изменится, если его строки поменять местами;	величина определителя не изменится, если его строки и столбцы поменять местами;
Укажите правильное утверждение:
если определитель имеет строку, равную столбцу, то он равен нулю;	если определитель имеет все строки, равные столбцам, то он равен нулю;	если определитель имеет две одинаковые строки (столбца), то он равен нулю;	если определитель имеет все одинаковые строки, то он равен нулю;
Укажите правильное утверждение:
если все элементы одной строки (столбца) определителя умножили на одно и то же число, то и определитель умножился на это число;	если все элементы одной строки (столбца) определителя умножили на одно и то же число, то определитель стал равен нулю;	если все элементы определителя умножили на одно и то же число, то и определитель умножился на это число;	если все элементы определителя умножили на одно и то же число, то определитель стал равен нулю;
Укажите правильное утверждение:
если все элементы определителя умножили на одно и то же число, то и определитель умножился на это число три раза;	если все элементы определителя умножили на одно и то же число, то и определитель умножился на это число n раз (n – порядок определителя);	если все элементы определителя умножили на одно и то же число, то и определитель умножился на это число, возведённое в степень n (n – порядок определителя);	если все элементы определителя умножили на одно и то же число, то и определитель умножился на это число в квадрате;
Укажите правильное утверждение:
если С=А·В, то \|С\|=\|A\|·\|B\|;	если \|С\|=\|A\|·\|B\|, где А и В — матрицы n-го порядка, то С=А·В;	если С=А·В, где А и В — матрицы n-го порядка, то \|С\|=\|A\|·\|B\|;	если \|С\|=\|A\|·\|B\|, где А и В — матрицы n-го порядка, то или С=А·В или С=В·А.