Определители квадратных матриц____________________________________________________

Определители квадратных матриц

Определитель — число, характеризующее квадратную матрицу А, обозначается |А| или detA или . В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение detA.

1. Определителем матрицы первого порядка А=(а), или определителем первого порядка, называется элемент а:

=|А|=|а|=а.

Например: |4|=4, |-3|=-3, |0|=0.

2. Определителем матрицы второго порядка 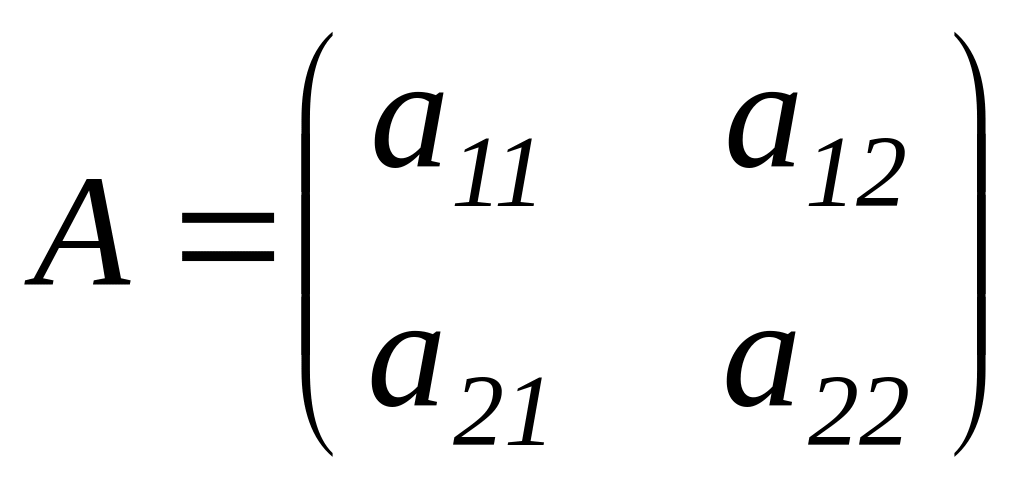, или определителем второго порядка, называется число, которое определяется по формуле:

Например:

3. Определителем матрицы третьего порядка 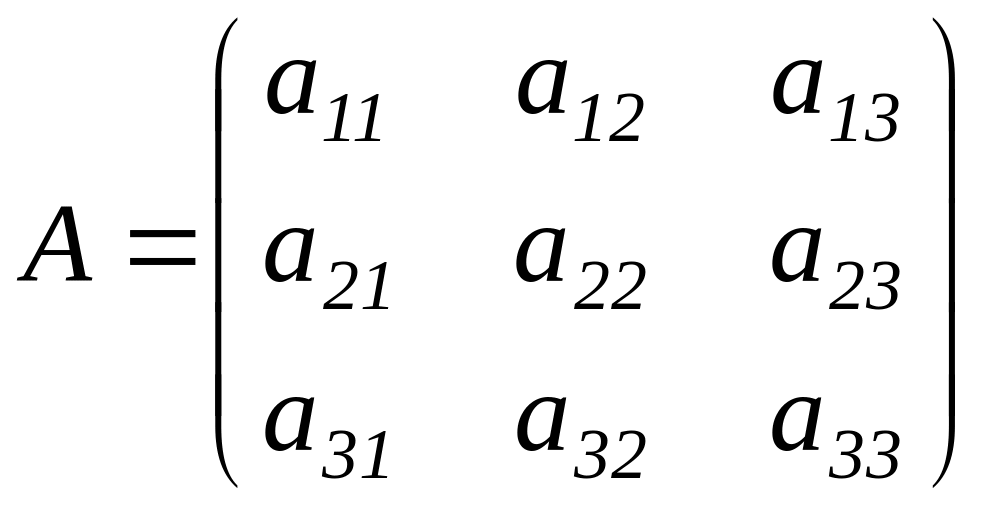, или определителем третьего порядка, называется число, которое определяется по формуле:

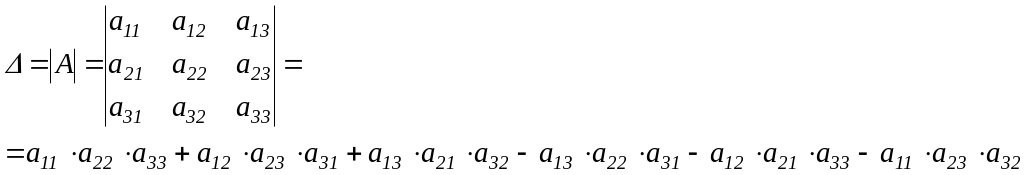
Для вычисления определителя третьего порядка пользуются правилами треугольника и параллелограмма:

Правило треугольника:

·	·	·			·	·	·		·	·	·
·	·	·	=	+	·	·	·	-	·	·	·
·	·	·			·	·	·		·	·	·

Правило параллелограмма:

·	·	·		+	·	·	·	-	1 строка
·	·	·	=	+	·	·	·	-	2 строка
·	·	·		+	·	·	·	-	3 строка
					·	·	·		1 строка
					·	·	·		2 строка

Правило параллелограмма:

				+	+	+
·	·	·		·	·	·	·	·
·	·	·	=	·	·	·	·	·
·	·	·		·	·	·	·	·
				-	-	-
				1 столбец	2 столбец	3 столбец	1 столбец	2 столбец