Метод секущих
Еще одна модификация метода Ньютона
связана с приближенным вычисление
производной
в окрестности точки
по формуле
.
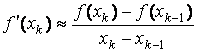Подставляя это выражение в формулу Ньютона, приходим к формуле
,
,
(2.20)
которая определяет метод секущих.
Название метода связано с его геометрической
интерпретацией. Секущая, проведенная
через точки
и
,
пересекает ось абсцисс в точке
,
значение которой определяется формулой
(2.20).
Д
ля
того, чтобы начать итерационный процесс
в методе секущих необходимо задать два
начальных приближения: нулевое
и первое
.
На практике, как правило, поступают
следующим образом: нулевое приближение
выбирают аналогично выбору начального
приближения в методе Ньютона, а в качестве
первого приближения выбирают величину
,
где e – заданная
погрешность. Эти значения используются
для нахождения последующего (второго)
приближения
по формуле (2.20). Затем, значения
и
используют для определения третьего
приближения
и т.д. Альтернативно, в качестве нулевого
и первого приближений могут быть выбраны
границы отрезка локализации корня, если
они известны. В этом случае первая
итерация метода секущий даст результат,
аналогичный методу хорд. Для завершения
итерационного процесса можно
воспользоваться условием (2.14).
Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной затруднено или невозможно, например, если функции получена в ходе численных расчетов, а не задана аналитически.
По алгоритму метод секущих близок к методу хорд, однако в отличие от последнего начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того при уточнении корня не проверяются знаки функции .
4.1. Постановка задачи
Во многих случаях встает проблема замены функции одной или многих переменных близкой ей функцией, чаще всего многочленом. Подобная задача может возникнуть в следующих ситуациях:
Решение задачи требует многократного вычисления значения функции в различных точках. Если задана громоздким аналитическим выражением, то для ускорения времени вычислений естественно заменить (аппроксимировать) исходную функцию близкой к ней функцией
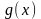так, чтобы
,
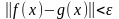где - точность аппроксимации. При этом вычисление должно быть более быстрой процедурой, чем вычисление . Во многих случаях в качестве выбирается полином некоторой степени.
Предположим, что функция задается своими значениями в узлах
.
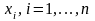В памяти эти значения хранятся в виде
двумерного массива
.
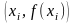При большом п
хранение и
обработка этой таблицы могут оказаться
слишком обременительными. В этом случае
проще подобрать близкую функцию
,
зависящую от небольшого числа параметров,
и работать не с табличными данными, а
с аналитическим выражением.Описанная выше таблица значений функции может представлять результаты какого-либо эксперимента. В этом случае перед экспериментатором стоит задача поиска эмпирической закономерности, наилучшим образом описывающей полученные результаты.
Во всех перечисленных случаях точность приближения зависит от введенной в качестве меры близости нормы. В зависимости от того, какая норма рассматривается, различают различные задачи аппроксимации.
Если в пространстве функций введена равномерная непрерывная норма
,
то задача называется задачей равномерного приближения.
Если рассматривается среднеквадратичная интегральная норма
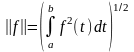
или согласованная с ней дискретная норма
,
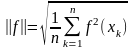то задача называется задачей среднеквадратичного приближения.