2.3. Метод простых итераций
Точные методы решения линейных систем применяются для систем относительно небольшой размерности (до 103). Для решения систем больших размерностей применяются итерационные методы, в частности, метод простых итераций.
Метод состоит в
том, что система уравнений
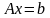преобразуется к виду
,
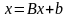и ее решение находится как предел
последовательности
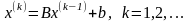
Теорема 2.1.
Пусть имеется система линейных уравнений
вида
(где С
- невырожденная квадратная матрица).
Предположим,
-
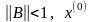произвольный вектор (начальное
приближение). Построим последовательность
векторов
- последовательные приближения (итерации).
В указанных условиях
решение системы существует и единственно;
при этом последовательные приближения
сходятся
к решению x*
со скоростью геометрической прогрессии.
Доказательство.
Поскольку x* является решением матричного уравнения, то:
.
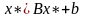(2.1)
.
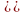Отсюда
а поскольку
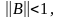то
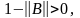следовательно,
.
Пусть система
однородна (b=0,
)
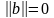. Тогда
.
Следовательно, в силу свойств нормы
однородная система имеет единственное
нулевое решение, поэтому неоднородная
система также имеет единственное
решение.
Возьмем какое-либо приближение
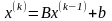(2.2)
и рассмотрим разность равенств (2.2) и (2.1):
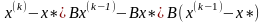(2.3)
Так как в силу свойств нормы
, (2.4)
то
.
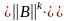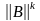- убывает со
скоростью геометрической прогрессии,
т.к.
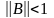по условию. Теорема доказана.
Произвольную систему вида Ax = b можно привести к виду, требуемому для применения метода простых итераций, положив B = A-E.
Действительно, Ах = (А – Е + Е)х = (А - Е)х + Ех = Вх + х = b.
Отсюда: х = b – Вх.
Оценим погрешность метода простых итераций. Учитывая (2.3), имеем:
,
.
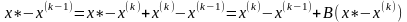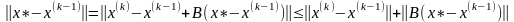
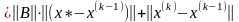Отсюда
.
Так как по условию
,
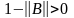то на это выражение можно делить:
.
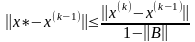Поскольку (см. (2.4))
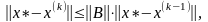
то
.
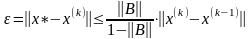2.4. Метод Зейделя
Пусть дана система
уравнений
.
Предположим, что все диагональные
элементы матрицы А
отличны от нуля: (
,
).
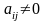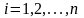Поделим каждое i -тое уравнение на aii :
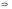
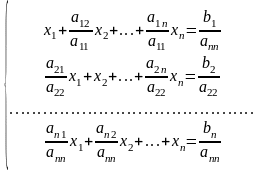
В правой части каждого из уравнений оставим только i–е неизвестные :
,
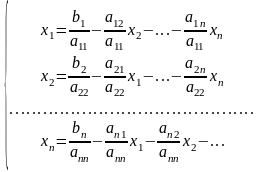Тогда система запишется в виде x = Cx + d , где
,
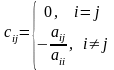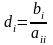
Выберем начальное
приближение
.
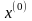Каждое следующее приближение вычисляется
по следующим формулам :
,
где
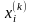- i-я
компонента k-го
приближения.
Данный метод похож
на метод простых итераций (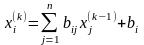
),
однако скорость сходимости метода
Зейделя выше, поскольку в процессе
вычислений используются уже найденные
компоненты более точного решения.
Теорема 2.2. Для сходимости метода Зейделя достаточно выполнение одного из двух условий :
а)
б) матрица А является положительно определенной, т.е. все ее собственные значения больше нуля.
2.5. Метод прогонки Метод прогонки используется для решения систем специального вида
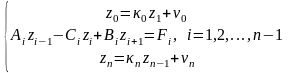
содержащих n+1 уравнение с неизвестными z0, z1, ..., z n .
Построим матрицу системы:
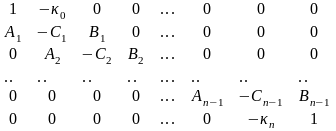
Основная система называется 3х-точечной разностной схемой, а первое и последнее уравнения – краевыми (граничными) условиями.
Предположим, что выполняются следующие условия:
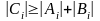
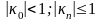
Рассмотрим первые два уравнения системы:
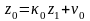(2.5)
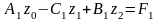(2.6)
Подставим (2.5) в (2.6):
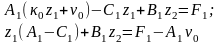
Выразим из полученного уравнения z1:
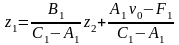
Произведем замену :
;
.
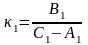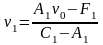Откуда следует,
что
.
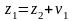Добавим к полученному уравнению третье уравнение системы, тогда выполнив аналогичные преобразования, получим уравнение для z2. Повторяя этот процесс, получим систему:
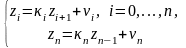(2.7)
где
;
,
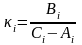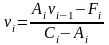i =1,
2, ..., n-1
Рассмотрим два последних уравнения получившейся системы.
.
Решим получившуюся систему уравнений по правилу Крамера:
;
;
.
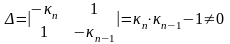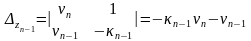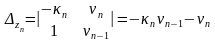Откуда находим неизвестные:
;
.
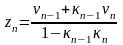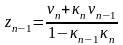Остальные неизвестные получаются последовательной подстановкой найденных значений в уравнения системы (2.7), начиная с (п-2)-го уравнения.
Процесс примедения системы к виду (2.7) называется прямым ходом метода прогонки. Процесс нахождения по ним неизвестных - обратным ходом метода прогонки.
Общее число выполняемых арифметических операций - 14п.