1.1. Метрические пространства

Метрическим пространством называется пара (Х, ), состоящая из некоторого множества (пространства) Х элементов (точек) и расстояния, т. е. неотрица­тельной действительной функции (х,у), определенной для лю­бых х и у из Х и подчиненной следующим трем аксиомам:

1) (х, у) = 0 тогда и только тогда, когда х = у,

2) (х, у) = (у, х) (аксиома симметрии),

3) (х, г) ≤ (х, у)+  (у, г) (аксиома треугольника).

Само метрическое пространство, т. е. пару (Х, ρ), мы будем обозначать, как правило, одной буквой: R = (X, ρ).

В случаях, когда недоразумения исключены, мы будем за­частую обозначать метрическое пространство тем же символом, что и сам «запас точек» X.

Приведем примеры метрических пространств. Некоторые из этих пространств играют в анализе весьма важную роль.

1. Положив для элементов произвольного множества

мы получим, очевидно, метрическое пространство. Его можно на­звать пространством изолированных точек.

2. Множество действительных чисел с расстоянием

ρ(х, у) = | х - у |

образует метрическое пространство R¹.

3. Множество упорядоченных наборов из п действительных чи­сел 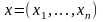с расстоянием

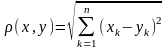
называется п-мерным арифметическим евклидовым пространством Rⁿ.

4. Рассмотрим то же самое множество наборов из п действительных чи­сел , но расстояние опре­делим в нем формулой

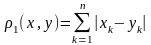
Справедливость аксиом 1)-3) здесь очевидна. Обозначим это метрическое пространство символом Rⁿ₁.

5. Возьмем снова то же самое множество, что и в приме­рах 3 и 4, и определим расстояние между его элементами фор­мулой

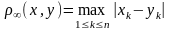
Справедливость аксиом 1)-3) очевидна. Это пространство, ко­торое мы обозначим Rⁿ_ во многих вопросах анализа не менее удобно, чем евклидово пространство Rⁿ.

Последние три примера показывают, что иногда и в самом деле важно иметь различные обозначения для самого метриче­ского пространства и для множества его точек, так как один и тот же запас точек может быть по-разному метризован.

6. Множество С [a, b] всех непрерывных действительных функ­ций, определенных на отрезке [a, b] с расстоянием

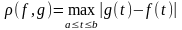
также образует метрическое пространство. Аксиомы 1)-3) про­веряются непосредственно. Это пространство играет очень важ­ную роль в анализе. Мы будем его обозначать тем же симво­лом С [a, b] , что и само множество точек этого пространства.

7. Рассмотрим, как и в примере 6, совокупность всех функ­ций, непрерывных на отрезке С [a, b], но расстояние определим иначе, а именно, положим

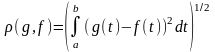
Такое метрическое пространство мы будем обозначать С₂[a, b] и называть пространством непрерывных функций с квад­ратичной метрикой.

1.3. Нормированные пространства

Пусть L - линейное пространство. Функция р, определенная на L, называется нормой, если она удовлетворяет следующим трем условиям:

1) р(х)  0, причем р(х) = 0 только при х = 0,

2) p(x + y)  p(x) + p(y), x,y  L.

3) р(x) = \\ р(х), каково бы ни было число .

Линейное пространство L, в котором за­дана некоторая норма, мы назовем нормированным простран­ством. Норму элемента x  L мы будем обозначать симво­лом .

Всякое нормированное пространство становится метрическим пространством, если ввести в нем расстояние

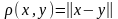
Справедливость аксиом метрического пространства тотчас же вытекает из свойств 1)-3) нормы. На нормированные про­странства переносятся, таким образом, все те понятия и факты, которые справедливы для метрических пространств.

Рассмотрим примеры нормированных пространств. Многие из пространств, рассматривавшихся в качестве примеров метрических пространств, в действительности могут быть наделены естественной структу­рой нормированного пространства.

1. Прямая линия R¹ становится нормированным пространством, если для всякого числа х  R¹ положить

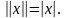
2. Если в действительном п-мерном пространстве Rⁿ с элементами положить

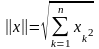
то все аксиомы нормы будут выполнены. Формула

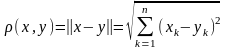
определяет в Rⁿ ту самую метрику, которую мы в этом про­странстве уже рассматривали.

В этом же линейном пространстве можно ввести норму

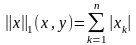
или норму

.

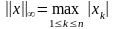Эти нормы определяют в Rⁿ метрики, которые мы рассматри­вали в примерах 4 и 5 п. 1. Проверка того, что в ка­ждом из этих случаев аксиомы нормы действительно выполнены, не составляет труда.

3. В пространстве С[a, b] непрерывных функций на отрезке [a, b] определим норму формулой

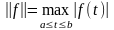
Соответствующая метрика уже рассматривалась в примере 6 п. 1.