3.8.2.Определение нулей и полюса замкнутой (по управлению и возмущению) системы {команда: “zpk(Wzam)”}

%Нули и полюса замкнутой системы по управлению%

zpk(Wzam)

%Поле нулей и полюсов замкнутой системы по управлению%

[p,z]=pzmap(Wzam)

%Нули и полюса замкнутой системы по возмущению%

zpk(Wvoz)

%Поле нулей и полюсов замкнутой системы по возмущению%

[p,z]=pzmap(Wvoz)

Zero/pole/gain:

243243.2432

--------------------------------

(s+105.3) (s^2 + 25.11s + 3735)

p = 1.0e+002 *

-1.0530

-0.1255 + 0.5981i

-0.1255 - 0.5981i

z = Empty matrix: 0-by-1

Zero/pole/gain:

0.55405 (s+3685) (s+47.13)

--------------------------------

(s+105.3) (s^2 + 25.11s + 3735)

p = 1.0e+002 *

-1.0530

-0.1255 + 0.5981i

-0.1255 - 0.5981i

z = 1.0e+003 *

-3.6846

-0.0471

Вывод: Об устойчивости можно судить по тому что все корни меньше нуля и находятся в отрицательной полуплоскости,а это значит что система устойчивая.

3.8.3.Найти поле нулей и полюсов замкнутой системы по управлению и возмущению

{команда: “[p,z]= pzmap(Wzam)”};

3.8.4. Построить годограф Найквиста и сделать вывод об устойчивости исходной системы {команда: “ nyquist(Wraz)”}

%Годограф Найквиста для разомкнутой системы%

nyquist(Wraz)

figure(1);

SUBPLOT(1,1,1), nyquist(Wraz);

Моделирование системы ТП-Д по передаточной фукции прим помощи MathLab.

Диаграмма Найквиста.

Вывод: Система устойчива, т.к мы наглядно видим, что годограф Найквиста разомкнутой системы не охватывает точку -1

3.8.5 Определить характеристики Боде, частоты среза и автоколебаний { команда: “ margin(Wraz)”};

%Характеристика Боде для разомкнутой системы%

margin(Wraz)

figure(2);

SUBPLOT(1,1,1), margin(Wraz);

3.8.6. График переходных процессов Ω=f(t) ,команды: t=[0: 0.001: 1]; [Ω,t]=step(Wzam*Uzad,t); plot(t,Ω),gridи t=[0: 0.001: 1]; [Ω,t]=step(Wraz*Ia,t); plot(t,Ω),grid.

%Переходный процесс по управлению%

t=[0:0.001:1];[y_1,t]=step(Wzam*Uzad,t);plot(t,y_1),grid;

%Переходный процесс по возмущению%

t=[0:0.001:1];[y_2,t]=step(Wvoz*Ia,t);plot(t,y_2),grid;

figure(3);

SUBPLOT(2,1,1),plot(t,y_1),grid;

SUBPLOT(2,1,2),plot(t,y_2),grid;

3.9. Моделирование системы в SIMULINK

3.9.1. Моделирование по схеме и по передаточной функции. Сравнение графиков переходных процессов

М оделирование системы ТП-Д по схеме:

М оделирование системы ТП-Д по передаточной функции

3.9.2.Частотные характеристики с использованием линейного анализа в SIMULINK

3.9.2.1Годограф Найквиста

Моделирование системы ТП-Д при помощи программы Simulink.

для исходной системы

.

Моделирование системы ТП-Д при помощи программы Simulink.

для режима автоколебаний когда характеристика проходит через -1

3.9.2.2 Характеристика Боде

Моделирование системы ТП-Д при помощи программы Simulink.

для исходной системы

Моделирование системы ТП-Д при помощи программы Simulink.

для режима автоколебаний

3.9.3 График переходного процесса: Ω=f(t) при управлении и возмущении.

при управлении

при возмущении

3.9.4. Проанализировать максимальные значения напряжения, тока и скорости и ввести соответствующие ограничения. Построить соответствующие графики .

Скорректированная схема (САУ) ТП-Д и графики напряжения, тока и скорости без ограничением координат по управляющему воздействию

Скорректированная схема САУ ТП-Д и графики напряжения, тока и скоростибез ограничением координат по возмущающему воздействию

Скорректированная схема (САУ) ТП-Д и графики напряжения, тока и скорости с ограничением координат по управляющему воздействию

Скорректированная схема (САУ) ТП-Д и графики напряжения, тока и скорости с ограничением координат по возмущающему воздействию

Вывод:

Выполнен расчет системы автоматического управления (САУ) с исполнительным механизмом приводимым электродвигателем постоянного тока, который питается от тиристорного преобразователя. Расчет показал, что параметры САУ удовлетворяют техническим требованиям предъявляемым к системе, а именно:

1)

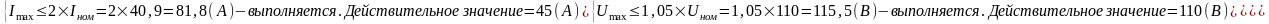
2) - выполняется:

- укладываемся в допустимые пределы;