§ 3. Невырожденные матрицы

1. . Основные понятия

Пусть А − квадратная матрица п-го порядка

.

Квадратная матрица А называется невырожденной, если ее определитель не равен нулю: ∆ = det A ≠ 0, и вырожденной – в противном случае.

Матрицей, союзной (присоединенной) к матрице А, называется матрица

,

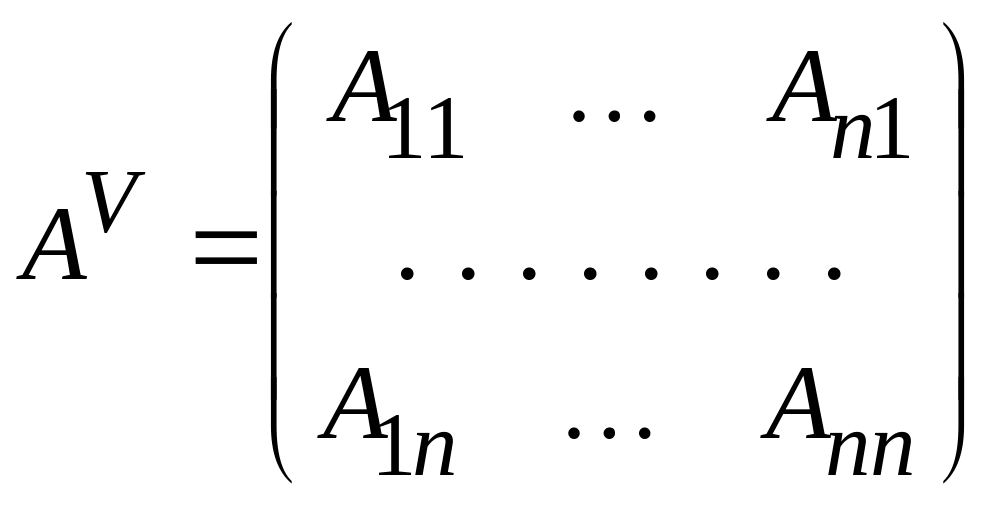составленная из алгебраических дополнений к элементам матрицы А, причем алгебраическое дополнение к элементу стоит на месте (ji), т.е. на пересечении j-й строки и i-го столбца.

Матрица называется обратной к матрице А, если выполняется условие

= = Е,

где Е − единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

2. Обратная матрица

Теорема 3.1 (О существовании обратной матрицы). Если А – невырожденная квадратная матрица, то она имеет единственную обратную матрицу, получающуюся из присоединенной делением всех ее элементов на det A:

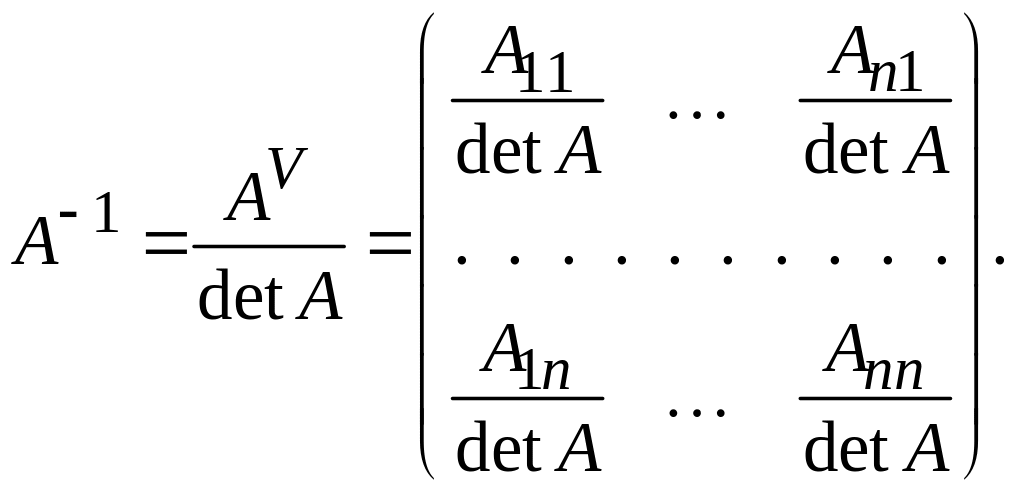(3.1)

 Проведем доказательство для случая матрицы 3-го порядка. Пусть

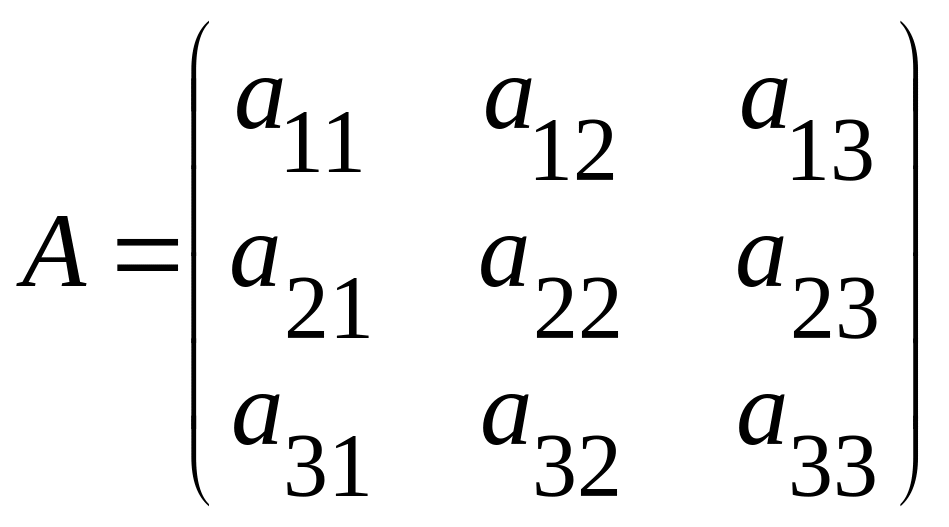, причем det А ≠ 0.

Составим союзную матрицу

и найдем произведение матриц А и :

А ∙ = ∙ =

=

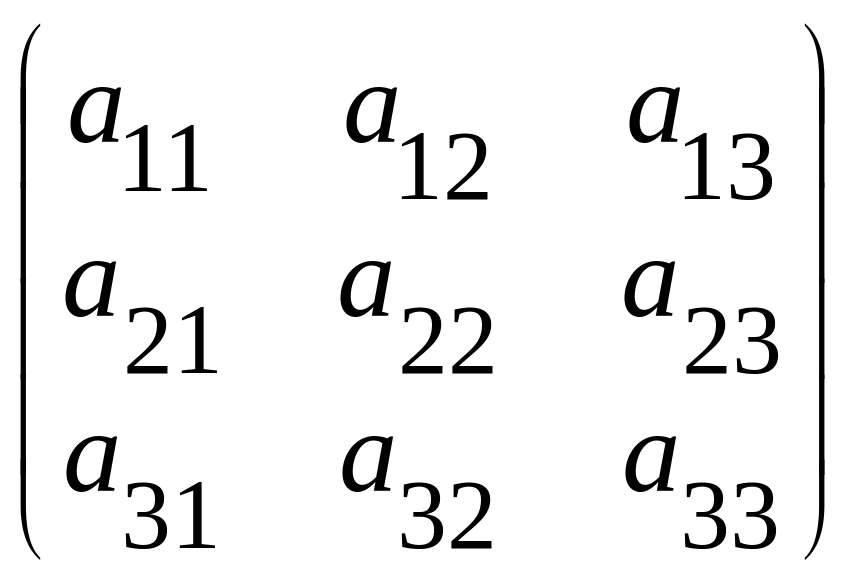= detA ∙ = det A ∙ E,

т.е. А ∙ = det A ∙ E. (3.2)

Аналогично убеждаемся, что

∙ А = det A ∙ E. (3.3)

Равенства (3.2) и (3.3) перепишем в виде

и .

Сравнивая полученные результаты с определением (3.1), получаем

, т.е. . ■

Отметим свойства обратной матрицы:

1. det( ) = ;

2. ;

3. .

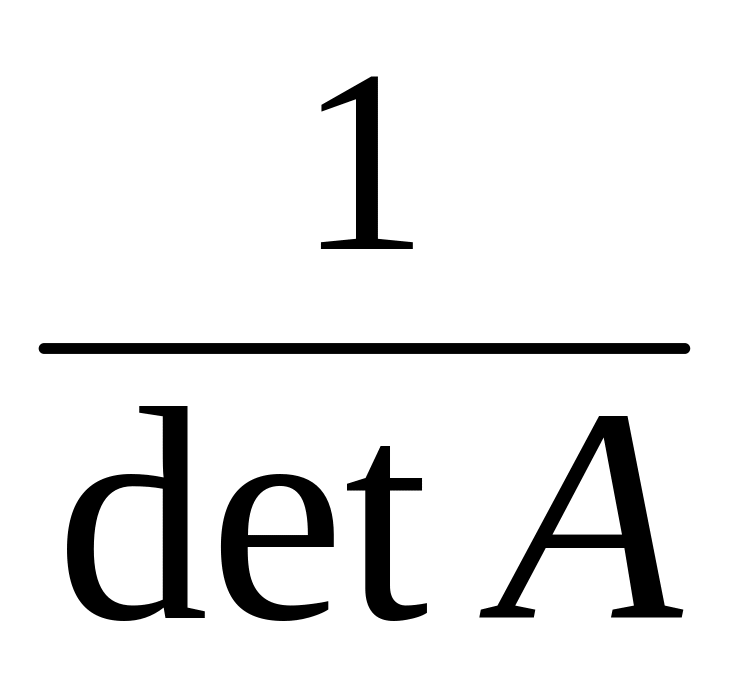3.3 Ранг матрицы

Рассмотрим матрицу А размера m×n.

.

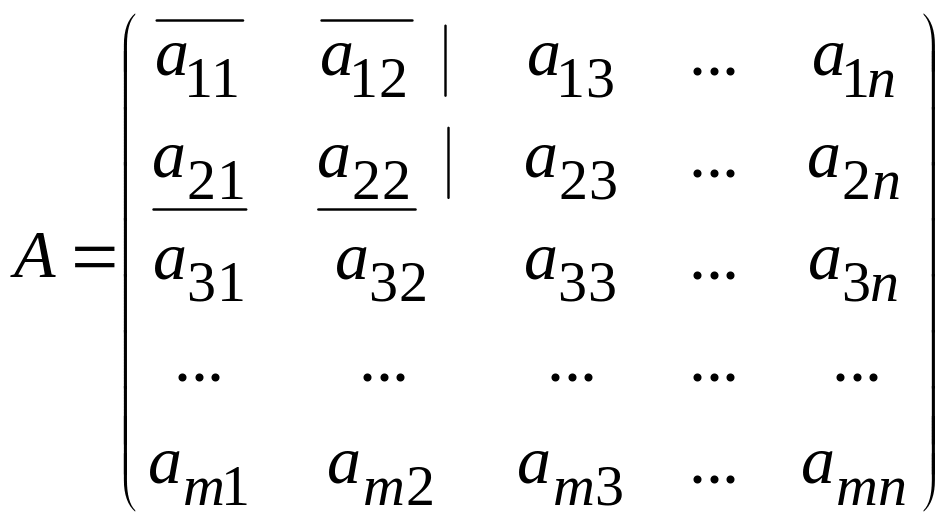Выделим в ней k строк и k столбцов (k ≤ min (m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами

этой матрицы. В матрице А пунктиром выделен минор 2-го порядка.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(A) или rang A.

Очевидно, что 0 ≤ r ≤ min (m;n), где min (m;n) – меньшее из чисел m и n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

§ 4. Системы линейных уравнений

4.1. Основные понятия

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

где , называются коэффициентами системы, числа - свободными членами.

Такую систему удобно записывать в компактной матричной форме

.

Коэффициенты этих уравнений записываются в виде матрицы А, называемой основной матрицей системы, а числа, стоящие в правой части системы, образуют столбец В, называемый столбцом свободных членов:

, .

Определение 1.11. Совокупность чисел называется решением системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел вместо неизвестных .

Системы, не имеющие решения, называются несовместными.

Системы, имеющие решения, называются совместными. Заметим, что система может иметь единственное решение, а может иметь бесконечно много решений.

Одна из задач линейной алгебры состоит в том, чтобы найти метод, позволяющий определить, совместна система или нет, а в случае совместности найти все решения системы.

Изложенная выше теория определителей позволяет исследовать на совместность системы, имеющие одинаковое количество уравнений и неизвестных.

Теорема 1.2 (Крамера). Система n уравнений с n неизвестными

имеет единственное решение, если определитель матрицы системы отличен от нуля. Это решение находится по формулам Крамера:

(1.7)

где  – определитель матрицы системы, а _k – определитель матрицы, полученной из матрицы системы заменой k-го столбца столбцом свободных членов.

Пример. Решить систему

Решение. Вычислим определители:

.

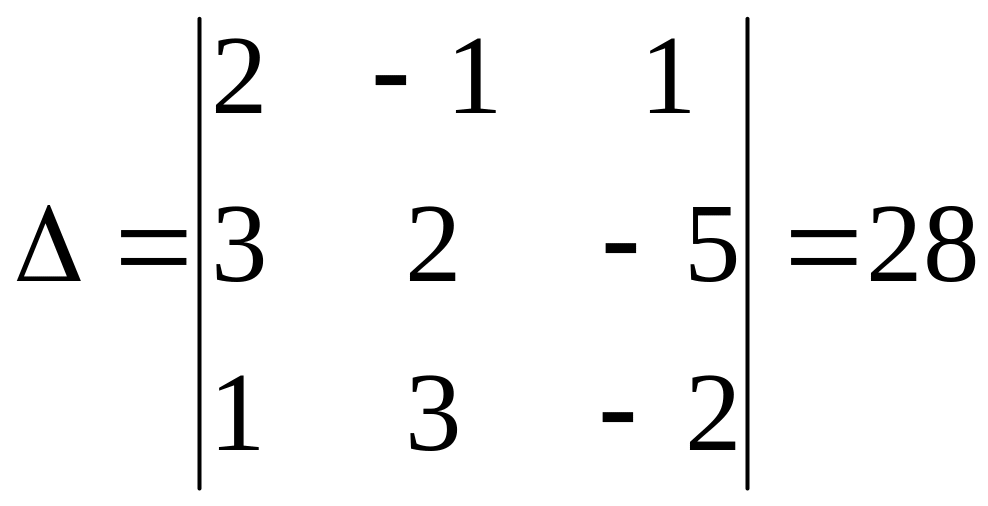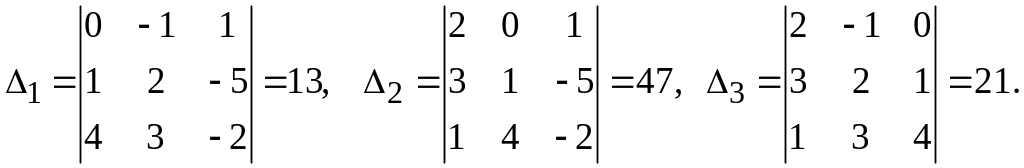
Так как Δ отличен от нуля, то система совместна, тогда решения системы:

.