
- •Элементы линейной алгебры
- •§ 1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§ 2. Определители
- •2.1. Основные понятия
- •2.2. Свойства определителей
- •§ 3. Невырожденные матрицы
- •. Основные понятия
- •Обратная матрица
- •3.3 Ранг матрицы
- •§ 4. Системы линейных уравнений
- •4.1. Основные понятия
- •Обратная матрица. Решение матричных уравнений Матричный метод решения систем линейных уравнений
- •Теоремы о существовании и единственности решения системы
- •Системы линейных неоднородных уравнений
- •Метод Гаусса решения систем линейных уравнений
- •Контрольные вопросы:
- •Лекция № 2. Векторная алгебра
- •2.1. Векторы. Линейные операции над ними. Разложение векторов. Вектор на оси
- •Вектор на плоскости и в пространстве
- •Декартовы координаты на плоскости и в пространстве
- •Базис. Разложение вектора по базису
- •Линейные операции в координатной форме
- •2.2. Скалярное произведение векторов
- •2.3. Векторное произведение векторов
- •2.4. Смешанное произведение векторов
- •Контрольные вопросы
- •Лекция № 3. Аналитическая геометрия
- •3.1. Прямая на плоскости. Ее уравнения
- •1. Общее уравнение прямой.
- •2. Неполные уравнения прямой.
- •3. Уравнение прямой в отрезках.
- •4. Каноническое уравнение прямой.
- •7. Параметрические уравнения прямой.
- •8. Прямая с угловым коэффициентом.
- •9. Нормальное уравнение прямой.
- •Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми
- •3.2. Виды уравнений плоскости
- •1. Общее уравнение плоскости.
- •2. Неполные уравнения плоскости.
- •3. Уравнение плоскости в отрезках.
- •4. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной данному вектору и проходящей через две данные точки
- •6. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •8. Нормальное уравнение плоскости.
- •3.3. Виды уравнений прямой в пространстве
- •1. Общие уравнения прямой.
- •2. Канонические уравнения прямой.
- •1) Точку , лежащую на этой прямой. Ее можно найти, взяв в уравнениях (3.28), например, и найдя и из системы:
- •4. Параметрические уравнения прямой.
- •Взаимное расположение прямых и плоскостей в пространстве
- •Контрольные вопросы
- •Лекция № 4. Предел числовой последовательности и функции
- •4.1. Предел числовой последовательности
- •Свойства предела последовательности
- •Бесконечно малые и бесконечно большие величины
- •Монотонная ограниченная последовательность
- •Критерий Коши существования предела последовательности
- •4.2. Предел функции
- •Предел функции на бесконечности
- •Предел функции в точке
- •Бесконечно большие функции
- •Свойства предела функции
- •Односторонние пределы
- •Критерий Коши существования предела функции
- •Замечательные пределы
- •Виды неопределенностей
- •Сравнение бесконечно малых
- •4.3. Непрерывность функции Непрерывность функции в точке
- •Необходимое и достаточное условие непрерывности функции в точке
- •Функции, непрерывные на отрезке
- •Контрольные вопросы
- •Лекция № 5. Производная функции и ее приложения
- •5.1. Определение производной функции. Ее геометрический и физический смысл
- •5.2. Дифференциал функции
- •5.3. Правила дифференцирования. Свойства дифференциала. Таблица производных
- •Свойства дифференциала
- •5.4. Дифференцирование обратных, неявных и параметрически заданных функций. Логарифмическое дифференцирование Дифференцирование обратных функций
- •Производная функции, заданной параметрически
- •5.5. Формула приближенного вычисления. Производные высших порядков
- •Формула приближенного вычисления
- •Производные высших порядков
- •Формула Лейбница
- •5.6. Приложения производной функции
- •Правило Лопиталя
- •Раскрытие неопределенностей вида () ()
- •Монотонность функции
- •Исследование функции на экстремум
- •Контрольные вопросы
5.2. Дифференциал функции
Для
функции y
= f(x)
рассмотрим производную
![]() Отсюда, по определению предела, величина
Отсюда, по определению предела, величина
![]() является бесконечно малой. Тогда
является бесконечно малой. Тогда
![]() или
или
![]() ,
где А = f′(x)
– константа. Таким образом, приращение
∆y
отличается от величины
,
где А = f′(x)
– константа. Таким образом, приращение
∆y
отличается от величины
![]() на бесконечно малую величину
на бесконечно малую величину
![]() более
высокого порядка, чем ∆x.
более
высокого порядка, чем ∆x.
Определение
5.2. Функция называется дифференцируемой
в точке х, если ее приращение
![]() в этой точке можно записать в виде:
.
в этой точке можно записать в виде:
.
Величина А∆x называется дифференциалом функции f(x) и обозначается dy = А∆x = f′(x) ∆x.
Величина
![]() называется дифференциалом
независимой переменной
и обозначается
называется дифференциалом
независимой переменной
и обозначается
![]() .
Тогда
.
Тогда
![]() (5.2)
(5.2)
Теорема 5.2. Функция f (x) дифференцируема в точке х тогда и только тогда, когда она имеет производную в этой точке, равную А.
Заметим, что мы можем рассматривать производную, как отношение двух дифференциалов:
![]() (5.3)
(5.3)
Операция нахождения производной функции называется дифференцированием функции.
5.3. Правила дифференцирования. Свойства дифференциала. Таблица производных
1)
Производная константы равна нулю, т.е.
![]() .
.
2) Если функция f (х) имеет производную в точке х, то С∙f (х) также имеет производную в точке х, и при этом
![]() (5.4)
(5.4)
3) Если функции и(х) и v(x) имеют производные в точке х, то их сумма f (х) = и(х) + v(x) также имеет производную в точке х, и при этом
![]() (5.5)
(5.5)
4) Если функции и(х) и v(x) имеют производные в точке х, то их произведение f(x) = u(x)v(x) также имеет производную в точке х и
![]() (5.6)
(5.6)
5)
Если функции и(х)
и v(x)
имеют производные в точке х
и, кроме
того, v(x)
0, то частное
![]() также имеет производную в точке x
и
также имеет производную в точке x
и
 (5.7)
(5.7)
6) Пусть дана сложная функция у = f (u), где и = g (x) и пусть u = g (x) имеет производную в точке х, а функция y = f (u) имеет производную в точке и = g (x). Тогда сложная функция у = f (g(х)) имеет производную в точке х и
![]() (5.8)
(5.8)
Свойства дифференциала
dc = 0, c = const.
d(u v) = du dv.
d(cu) = c du, c = const.
d(uv) = v du + udv.
![]() .
.
Дифференциал сложной функции: если
y = f(x),
x = φ(t),
то
![]() .
.
Инвариантность
формы первого дифференциала
относительно выбора переменных:
дифференциал функции равен произведению
производной этой функции на дифференциал
аргумента, при этом безразлично, будет
ли этот аргумент независимой переменной
или функцией от другой независимой
переменной.
Таким образом, если
![]() и
и
![]() ,
то
,
то
![]() .
Тогда свойство инвариантности выражается
формулой:
.
Тогда свойство инвариантности выражается
формулой:
![]() (5.9)
(5.9)
Таблица производных основных элементарных функций (таб. 5.1)
Таблица 5.1

Примеры.

2.
![]() .
Воспользуемся правилом дифференцирования
произведения функций:
.
Воспользуемся правилом дифференцирования
произведения функций:
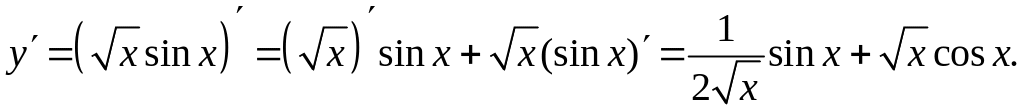
3.
![]() .
Воспользуемся
правилом дифференцирования частного
функций:
.
Воспользуемся
правилом дифференцирования частного
функций:

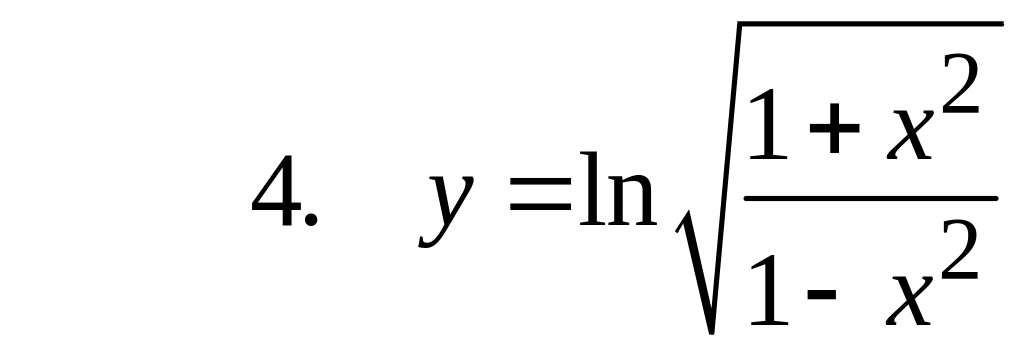 .
Так
как эта функция сложная, то воспользуемся
правилом дифференцирования сложной
функции:
.
Так
как эта функция сложная, то воспользуемся
правилом дифференцирования сложной
функции:

5.4. Дифференцирование обратных, неявных и параметрически заданных функций. Логарифмическое дифференцирование Дифференцирование обратных функций
Теорема
5.3. Пусть
![]() – непрерывная, строго возрастающая
или строго убывающая в некоторой
окрестности точки х,
и пусть в этой точке существует
производная
– непрерывная, строго возрастающая
или строго убывающая в некоторой
окрестности точки х,
и пусть в этой точке существует
производная
![]() .
Тогда обратная функция
.
Тогда обратная функция
![]() также имеет производную в точке
,
причем выполняются формулы
также имеет производную в точке
,
причем выполняются формулы
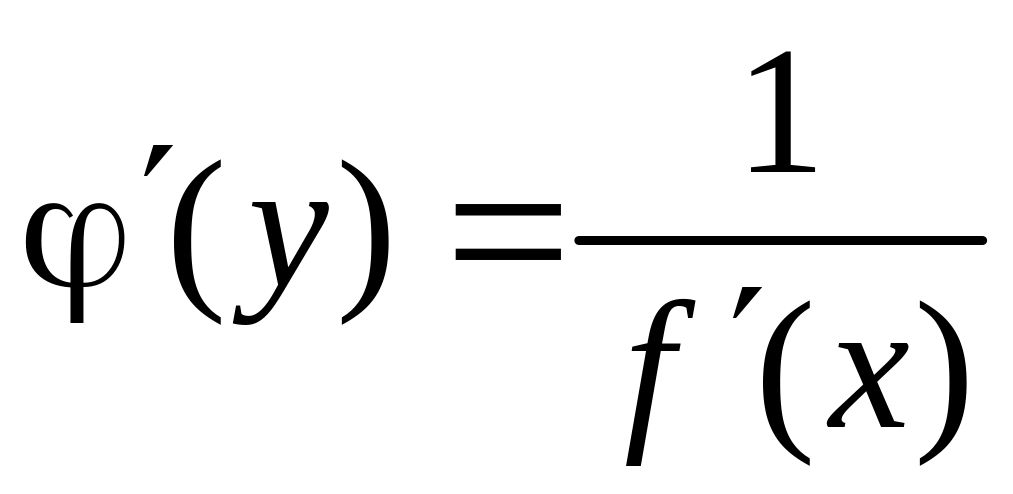 или
или
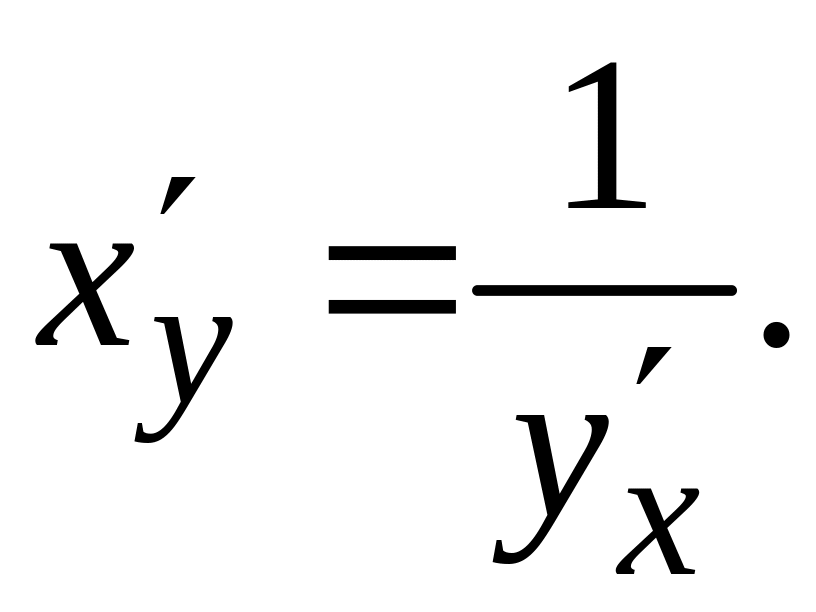 (5.10)
(5.10)
С помощью этой теоремы получаются формулы для производных обратных тригонометрических функций и логарифмической функции.
Производная неявной функции
Определение 5.3.
Говорят, что уравнение
![]() задает функцию
неявно,
если существует множество Е,
такое что для любого
задает функцию
неявно,
если существует множество Е,
такое что для любого
![]() существует по крайней мере одно у,
удовлетворяющее уравнению
.
Одно и то же уравнение может задавать
не одну, а несколько функций.
существует по крайней мере одно у,
удовлетворяющее уравнению
.
Одно и то же уравнение может задавать
не одну, а несколько функций.
Дифференцируя
уравнение
по х
и учитывая, что у
зависит от х,
можно найти производную
![]() .
.
Логарифмическая производная
Определение
5.4. Пусть
дана функция
.
Логарифмической
производной
этой функции называется производная
от натурального логарифма этой функции.
А именно,
 .
.
Производная сложно-степенной (сложно-показательной) функции
Определение
5.5. Функция
вида
![]() называется сложно-степенной
или сложно-показательной
функцией.
называется сложно-степенной
или сложно-показательной
функцией.
Для того чтобы продифференцировать ее, воспользуемся логарифмической производной. Имеем

Так
как
 ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
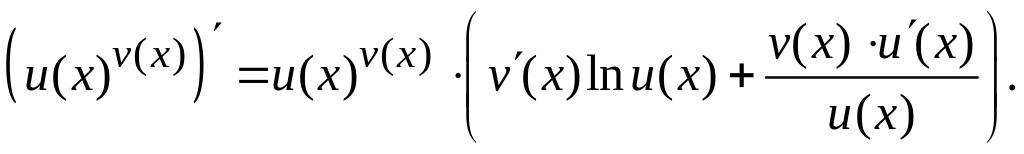 (5.11)
(5.11)
Пример. Найдем производную функции у = (sin x)x .
Решение. Имеем ln у = ln (sin x)x = х ln sin x,
(ln
y)
= x
ln (sin x)
+ x
(ln
(sin
x))
= ln (sin x)
+
![]() = ln (sin x)
+
x
ctg
x,
= ln (sin x)
+
x
ctg
x,
тогда у' = (sin x)x (ln (sin x) + xctg x).
