Контрольные вопросы

1. Общее уравнение прямой, неполные уравнения прямой, уравнение прямой в отрезках.

2. Каноническое уравнение прямой, уравнение прямой, проходящей через две заданные точки, уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору.

3. Параметрические уравнения прямой, уравнение прямой с угловым коэффициентом, нормальное уравнение прямой.

4. Расстояние от точки до прямой.

5. Условия параллельности и перпендикулярности прямых, заданных общими уравнениями. Нахождение угла между этими прямыми.

6. Условия параллельности и перпендикулярности прямых, заданных в виде с угловым коэффициентом. Нахождение угла между этими прямыми.

7. Общее уравнение плоскости, неполные уравнения плоскости, уравнение плоскости в отрезках.

8. Уравнение плоскости, проходящей через три точки, Уравнение плоскости, параллельной заданному вектору и проходящей через две заданные точки, уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через заданную точку.

9. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

10. Общие, канонические и канонические уравнения прямой в пространстве. Уравнения прямой, проходящей через две заданные точки.

11. Условия параллельности и перпендикулярности прямой и плоскости. Вычисление угла между прямой и плоскостью.

12. Условия параллельности и перпендикулярности двух прямых. Вычисление угла между прямыми.

13. Условия параллельности и перпендикулярности двух плоскостей. Вычисление угла между плоскостями.

Лекция № 4. Предел числовой последовательности и функции

4.1. Предел числовой последовательности

Определение 4.1. Пусть каждому натуральному числу приведено в соответствие число . Тогда говорят, что задана числовая последовательность и обозначают ее .

Числа называются элементами последовательности, а выражение – общим членом последовательности.

Примеры.

1. .

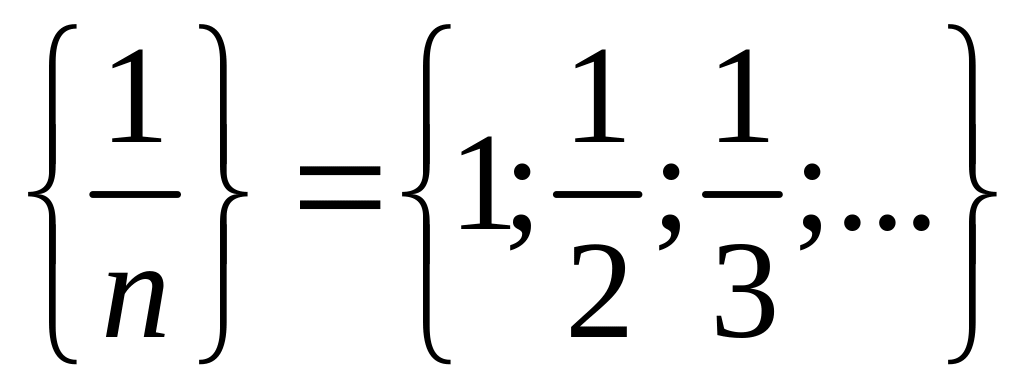2. .

Определение 4.2. Последовательность называется ограниченной, если существует число М, такое, что .

Последовательность называется ограниченной сверху (снизу), если существует число М, такое, что .

Определение 4.3. Число а называется пределом числовой последовательности , если для любого  > 0 найдётся натуральное число N такое, что для  п > N выполняется неравенство | х_n - а | < . Или, используя краткую запись,

  > 0  N  n > N | х_n - а | < .

В этом случае пишут или х_n  а и говорят, что х_n стремится к а или последовательность сходится к а.

Если последовательность имеет конечный предел, то говорят, что она сходится. Если последовательность не имеет конечного предела, то ее называют расходящейся.

Определение 4.4. Интервал , содержащий в себе точку а, называется окрестностью точки а.

Интервал (a - , a + ) также будет окрестностью точки а. Он называется -окрестностью точки а. При этом неравенство | х_n - а | <  может быть переписано в виде: (a - , a + ).

Понятие предела является базовым понятием математического анализа. Сформулируем определение предела последовательности по-другому.

Определение 4.5. Число а называется пределом числовой последовательности , если любая -окрестность точки а содержит все члены последовательности х_n, начиная с некоторого номера N (см. рис. 4.1).

Рис. 4.1

Отметим, что номер N в определении предела, вообще говоря, зависит от ε. Чем меньшую -окрестность приходится рассматривать, тем более удаленные точки последовательности приходится брать.