Элементы линейной алгебры

§ 1. Матрицы

1. Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

А = или, сокращенно А = ( ),

где ί = 1,2,3,…, m − номер строки, j = 1,2,3,…, n − номер столбца.

Числа называются элементами матрицы. Таким образом, первый индекс элемента указывает на номер строки, второй – на номер столбца, на пересечении которых стоит этот элемент. Если m=n, т.е. число строк матрицы равно числу столбцов, то матрица называется квадратной матрицей порядка n.

Диагональ квадратной матрицы, составленная из элементов a₁₁, a₂₂, …, a_nn, называется главной диагональю.

Квадратная матрица называется единичной, если на главной диагонали у нее стоят единицы, а остальные элементы – нули.

Матрица, все элементы которой равны нулю, называется нулевой.

Матрица, содержащая один столбец или одну строку, называется вектором.

Пусть дана произвольная матрица

.

Матрица , у которой каждая строка является столбцом матрицы А с тем же номером (и, следовательно, каждый столбец является строкой матрицы А), называется транспонированной к матрице А. Переход от матрицы А к В называется транспонированием. Будем обоз­на­чать транспонированную матрицу А^Т.

Заметим, что .

Матрицы А и В одинаковых размеров nm с элементами и

называются равными, если для i= 1, 2,…, n, j = 1, 2, …, m. Равенство матриц обозначается А = В.

2. Действия над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц А и В одинаковых размеров nm с элементами и называется матрица С = А + В, элементы которой получаются путем сложения соответствующих элементов данных матриц: для i = 1, 2, …, n, j = 1, 2, …, m.

Определенное таким образом сложение будет, очевидно, коммутативным и ассоциативным.

Разность матриц А – В можно определить так: А – B = A +( – B ).

Умножение на число

Произведением матрицы А = ( ) на число  называется матрица С =   А, элементы которой получаются умножением элементов матрицы А на число : , где i = 1, 2, …, n, j = 1, 2, …, m.

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1. А + В = В + А; 5. 1 · A = A;

2. А + ( B + C ) = ( A + B ) + C; 6. α · ( A + B ) = αA + αB;

3. A + O = A; 7. (α + β ) · A = αA + βA;

4. A – A = O; 8. α · ( βA ) = ( αβ ) · A,

где А, B, C − матрицы, α и β − числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• перестановка местами двух параллельных рядов матрицы;

• умножение всех элементов ряда матрицы на число, отличное от нуля;

• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований, А ~ В.

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А размера mn с элементами и матрицы

В размера np с элементами называется матрица С = АВ размера mp c элементами , если

(1.1)

где i = 1, 2, …, m, j = 1, 2, …, p.

Пример1.1.

.

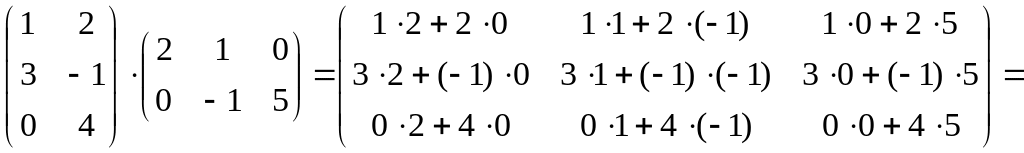
Матрицы А и В называются перестановочными, если АВ = ВА.

Умножение матриц обладает следующими свойствами, если суммы и произведения матриц имеют смысл:

1. А  В  В  А; 4. ( В + С )  А = В  А + С  А;

2. А ( В  С ) = ( А  В ) С; 5. α · ( AВ ) = ( αА ) · В.

3. А  ( В + С ) = А  В + А  С;

Для операции транспонирования верны свойства:

1. ;

2. .