Задача 2

Задача 1

Следующие задачи линейного программирования в стандартной форме, записанные в матричной форме, называются симметричной парой взаимно двойственных задач:

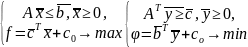
Здесь

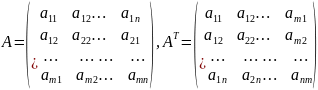
• Матрица коэффициентов и транспонированная матрица;

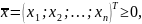
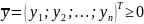- столбцы неотрицательных неизвестных;

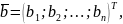
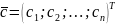– столбцы правых частей; 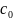– константа.

Решение задач 1 и 2 взаимосвязаны. Решив любую из них (исходную задачу), можно восстановить решение другой (двойственной задачи).

Первая теорема двойственности.

Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны:

Вторая теорема двойственности. Оптимальные решения

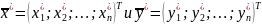
пары двойственных задач связаны между собой следующими соотношениями:

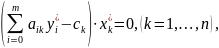
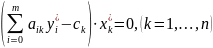
Замечание.

Если исходная задача неразрешима из-за неограниченности целевой функции, то двойственная задача неразрешима из-за отсутствия допустимых значений.

Двойственность в экономико-математических моделях.

Каждая задача ЛП может быть поставлена с помощью другой задачи ЛП, которая имеет свой экономический смысл. Этот смысл в какой-то мере противоположен смыслу прямой (исходной) задачи.

Например, если исходная задача была на нахождение максимальной прибыли при ограничениях на ресурсы, то двойственная будет на нахождение минимальной стоимости сырья, при котором его можно продавать, а не пускать в производство, чтобы получить наименьшую прибыль. Решая одну из взаимнодвойственных задач, можно автоматически получить решение второй задачи.

22. Закон инерции квадратичных форм. Критерий Сильвестра знакоопределенности квадратичной формы.

Закон инерции квадратичных форм: число р положительных коэффициентов и число q отрицательных коэффициентов в нормальном виде формы ранга r не зависят от способа приведения квадратичной формы к нормальному виду; r=p+q.

Критерий Сильвестра. Квадратичная форма является положительно определенной, когда все угловые миноры ее матрицы положительны. Квадратичная форма является отрицательно определенной тогда и только тогда, когда знаки угловых миноров ее матрицы чередуются. Опр1<0, опр2>0, опр3<0

23. Прямая и гиперплоскость в n-мерном пространстве. Угол между гиперплоскостями. Расстояние от точки до гиперплоскости.

1. Прямая в n-мерном прост-ве

Опр. Пусть А(a₁, a₂,.. a_n) – фиксированная(фикс.) точка(т.) из точечного прост-ва Т и p҃(p₁, p₂,.. p_n) - фикс. вектор из векторного прост-ва V, отличной от 0҃. Множество т. вида X=A+tp҃ (где t - любое число) называется прямой, проходящей через т. А по направлению вектора p҃, или просто прямой.

Равенство(знак системы) X₁= a₁+ tp҃₁

X₂= a₂+ tp҃₂

X_n= a_n+ tp҃_n

Назыв. - параметрические уравнения прямой, p҃ - направляющий вектор

В 3-мерном прост-ве это обычная прямая, заданная параметрич. ур-ями

2. Гиперплоскость в n-мерном пространстве

Опр. Пусть k- натуральное число, А(a₁, a₂,.. a_n) – фикс. т. в n-мерном прост-ве T и p҃₁ , p҃₂, .. p҃_k – набор линейно независимых векторов из линейного прост-ва V. Множество т. вида X= A+ t₁ p҃₁+ t₂p҃₂+ t _k p҃ _k , где t₁ , t₂ , t _k – любые числа, назыв. k-мерной плоскостью в T.

Из линейной независимости указанных векторов следует, что 0kn.

При k=0 – это одна т.А.; при k=n n-мерная плоскость совпадает со всем пространством Т; при k=1(одномерн.плоск) это прямые. Пл-сти размерностью k=n-1 носят название гиперплоскости(Г.)

Г. в 3-мерном прост-ве - это обычная плоскость(рис 6.5), заданная ур-ем a₁ x₁+a₂ x₂+a₃ x₃+b=0

Теорема. Любая Г. в n-мерном прост-ве Т. состоит их точек Х(х₁ ,х₂ ,..х_n ), координаты которых удовлетворяют некоторому ур-ию первой степени: с₁ х₁+ с₂ х₂+…+ с_n х_n+b=0 ,где с₁ , с₂ ,.. с_n и b –фикс. числа, причем не с₁ , с₂ ,.. с_n равны нулю.

Взять доказательство из желто-рыжего учебника, с.190-191