1. Арифметический н-вектор-любая последовательность из действительных чисел а_1,а₂,….а_н.

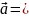(а₁,а₂,..а_n) векторное пространство Rⁿ-множество всех н-мерных арифметических векторов, в котором введены указанные ниже операции сложения и умножения векторов на число.

1) а+b=b+а

2) (а+b)+c=a+(b+c)

3) существует нулевой элемент 0, такой что

а+0=а для любого вектора а

4) для каждого элемента а сущ.-а, такой что а+(-а)=0

5) л(а+в)=ла+лв

6) (л+м)а=ла+ма

7) Л(ма)=(лм)а

8) 1*а=а, где а,в,с-произвольные элементы V; л,м-скаляры-произвольные действительные числа

2. Геометрический смысл пространств R2 и R3 . Линейные пространства. ГС имеют только R1,R2,R3. Для R1 – это прямая, для R2 – плоскость, для R3 – трехмерное пространство. множество V называют линейным или векторным пространством, а его элементы –векторами, если на нем определены операции:

• сложение векторов, означающее, что каждым двум а и в по некоторому правилу ставится в соответствие третий вектор, называемый суммой а и в, обозначаемый а+в

• умножение вектора на число, каждой паре, состоящей из а и числа Л, ставится в соответствие вектор, называемый Л на а и обозначаемый Ла. при этом требуется чтобы указанные операции удовлетворяли следующим условиям:

1. а+b=b+а

2. (а+b)+c=a+(b+c)

3. существует нулевой элемент 0, такой что а+0=а для любого вектора а

4. для каждого элемента а сущ.-а, такой что а+(-а)=0

5. л(а+в)=ла+лв

6. (л+м)а=ла+ма

7. Л(ма)=(лм)а

8. 1*а=а, где а,в,с-произвольные элементы V; л,м-скаляры-произвольные действительные числа.

3. Линейная зависимость системы векторов и ее геометрический смысл. а₁,а₂,….а_к-линейно зависимые, если сущ. Такие числа л1,л2,лк не равные 0 одновременно, что выполняется равенство л₁a₁+л₂а₂ …+л_kа_k= 0

Геометрический смысл линейной зависимости векторов очевиден в R2 b R3. В R2: векторы коллинеарные, в R3 компланарные( 3 линейно зависимых векторы параллельны одной плоскости) R2 R3

4. Базис и размерность линейного пространства. Координаты вектора в данном базисе.

Базис – линейно зависимая система векторов линейного пространства V, из которого любой вектор а является линейной комбинацией векторов данной системы, т.е

а=к₁ а₁ +а₂ к₂ +..к_c а_c-разложение вектора по данному базису,к₁,к₂,к_c-координаты вектора в данном базисе.

Размерность линейного пространства- число векторов его базиса.

5. Преобразование координат векторов при замене базиса. Подпространства линейного пространства.

Подмножество S линейного пространства V называется подпространством, если выполнены следующие условия: для любых а, в из S их а+в принадлежит S для любого а из S и любого действительного числа л произведение ла принадлежит S

6. Скалярное произведение векторов в Rn. Евклидово пространство. Длины векторов и угол между векторами в Rn .

На линейном пространстве V задано скалярное произведение, если имеется правило. По которому 2ум а и в сопоставляется число (а,в), удовлетворяющее 4 аксиомам: (а,в) = (в,а)

(Ка,в)=к(а,в)

(а+в, с)= (а,с) +(в,с)

(а,а)>0 ,если а не равно 0 и если (а,а)=0, то а=0 Евклидово пространство- линейное подпространство, на котором задано скалярное произведение.

Длина вектора определяется формулой: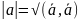

Косинус угла между векторами определяется формулой:

7. Ортогональный и ортонормированный базисы в Rn . Координаты вектора в ортогональном базисе.

Базис е₁,е₂,е_н евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е. (е­_I ,e_j) =0

Базис е1,е₂,е_n евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице.

8. Определение матрицы. Сложение матриц и умножение матрицы на число. Умножение матриц. Ранг матрицы. матрицей размера м*н называется прямоугольная таблица из чисел а_ij содержащая м столбцов и н строк.

Суммой матрицы А=(a_ij) и B=(b_ij) одного размера называется матрица А+В того же размера , определяемая равенством А+В=(а_ij+b_ij).

Произведением матрицы А( ) на число л, называется матрица ЛА=(Ла_ij).чтобы умножить матрицу на число, нужно все ее элементы умножить на это число . умножение матриц пусть даны две матрицы А м*н и В н*к тогда произведением матрицы А на В называется С размера м*к, каждый элемент которой С(I,j) скалярное произведение i-строки А на j-столбец В. А(a_1ia_2i a_ni) B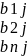 C_ij= a_i1*b_1j+a_i2*b_2j…+a_in*b_nj Ранг матрицы-система векторов образуемых строками матрицы А, т.е максимально число линейно независимых этой матрицы rk A.

9. Обратная матрица. Нахождение обратной матрицы с помощью элементарных преобразований. матрица А^-1 называется обратной к КВАДРАТНОЙ матрице А, если их произведение равно единичной матрице Е 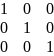пусть А-невырожденная матрица. Припишем к ней единичную матрицу Е .Далее с помощью эл. пр. над строками «сдвоенной» матрица (АIЕ) приводим левую половину то есть А к единичной матрице Е. тогда на месте первоначально приписанной Е окажется А^-1.

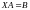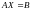10. Решение матричных уравнений вида и . Решением ХА=В будет ХАА^-1=ВА^-1 или Х= ВА^-1

Решением AX=B будет Х=А^-1В