3.2.2 Проверка однородности нескольких дисперсий, найденных по выборкам одинакового объема
Для проверки
однородности нескольких дисперсий при
равных объемах всех рассматриваемых
выборок
может быть использован G
- критерий
Кохрена.
Пусть
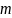- количество
выборочных дисперсий, однородность
которых проверяется. Обозначим эти
дисперсии
.
Вычисляется расчетное G
- отношение по
формуле
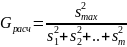
В числителе этой
формулы стоит наибольшая из рассматриваемых
дисперсий, а в знаменателе – сумма всех
дисперсий. Далее обращаются к таблицам
распределения Кохрена. По выбранному
уровню значимости q
, числу
степеней свободы каждой выборки
и по количеству
выборок
из этой таблицы отыскивают величину
.
Если
то можно принять гипотезу об однородности
дисперсий. В противном случае она
отвергается.
3.2.3 Проверка однородности средних
Здесь исследуются две выборки, имеющие различные средние арифметические. Данная проверка позволяет установить, вызвано ли расхождение между средними случайными ошибками измерения или оно связано с влиянием каких-либо неслучайных факторов. Эта процедура находит широкое применение, например, в случаях, если требуется установить идентичность параметров одинаковых изделий, изготавливаемых на разном оборудовании.
Проверка проводится
с применением
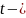критерия Стьюдента. Пусть
объемы выборок,
соответствующие средние,
оценки дисперсий, найденные по этим
выборкам.
Предстоит рассмотреть два случая.
1. Дисперсии однородны. Вычисляется расчетное отношение по формуле
Из таблиц
распределения Стьюдента при уровне
значимости
и числе степеней свободы
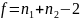находят табличное значение
.
Если
,
то расхождение между средними значимо.
В противном случае можно принять гипотезу
об однородности средних. Формула
упрощается, если обе выборки имеют
одинаковый объем, т. е.
.
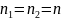В этом случае
2. Дисперсии неоднородны. Как и в предыдущем случае здесь можно использовать критерий Стьюдента, но формула для расчета имеет уже следующий вид:
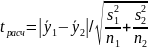
Далее вычисляют величину по формуле
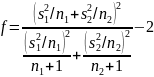
Найденное значение округляют до целого и принимают за число степеней свободы. По этой величине и по уровню значимости из таблиц распределения Стьюдента отыскивается . Дальнейший ход проверки не отличается от предыдущего случая.
*Примечание.
Табличное значение
критерия Фишера определяют, используя
встроенную статистическую функцию
FРАСПОБР
.
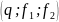3.3 Результаты расчетов
Таблица 5...7. - расчетный лист из Microsoft Excel части №3.
4 ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
4.1 Исходные данные
474 |
410 |
478 |
465 |
429 |
451 |
393 |
435 |
441 |
426 |
436 |
436 |
453 |
465 |
479 |
472 |
469 |
462 |
497 |
433 |
469 |
420 |
472 |
459 |
441 |
419 |
342 |
194 |
498 |
479 |
483 |
458 |
467 |
435 |
480 |
447 |
479 |
427 |
432 |
583 |
498 |
415 |
441 |
459 |
449 |
371 |
450 |
498 |
415 |
389 |
466 |
415 |
455 |
454 |
457 |
434 |
528 |
455 |
544 |
447 |
506 |
495 |
432 |
520 |
435 |
506 |
404 |
428 |
413 |
501 |
461 |
488 |
479 |
371 |
448 |
440 |
498 |
603 |
506 |
386 |
440 |
445 |
467 |
459 |
419 |
521 |
410 |
417 |
409 |
411 |
465 |
438 |
461 |
433 |
456 |
441 |
498 |
471 |
483 |
464 |
515 |
464 |
435 |
447 |
436 |
425 |
423 |
416 |
448 |
430 |
488 |
426 |
481 |
448 |
458 |
451 |
451 |
453 |
469 |
389 |
425 |
459 |
424 |
504 |
441 |
413 |
446 |
406 |
408 |
440 |
416 |
397 |
459 |
441 |
438 |
424 |
434 |
421 |
435 |
425 |
427 |
488 |
422 |
412 |
476 |
494 |
537 |
442 |
461 |
469 |
«Проверка гипотезы о нормальности распределения»
Вариант №2
В результате проведения разведывательных опытов была получена выборка. Проверить гипотезу о нормальности распределения.