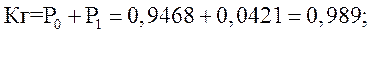4.2. Расчет коэффициента готовности энергоблока с т-турбиной в электроэнергетической системе.

         В основе метода расчета коэффициента готовности лежит описание функционирования энергоагрегата марковским процессом с дискретным множеством состояний.

Теплофикационный энергоблок представляется в виде простой структурной схемы из двух элементов: котла и турбогенератора (Рис.3а).

Достижимые состояния энергоблока из графа достижимых состояний (Рис. 3б):  =(0,0) –  энергоблок работоспособен (котел и турбина находятся в работе);

=(1,0) –  энергоблок не работоспособен (котел отказал, турбогенератор работоспособен);

=(0,1) –  энергоблок не работоспособен (котел работоспособен, турбогенератор отказал);

=(1,1) – когда одновременно отказали и котел и турбогенератор. Недостижимо, т.к. одновременное наступление указанных событий (с точки зрения теории вероятностей)  невозможно. 

                                    а)                                                               б)

Рис.3. Структурная схема (а) и граф достижимых состояний энергоблоков (б):

1 – котел; 2 – турбогенератор;   – достижимые состояния.

Система дифференциальных уравнений для расчета вероятностей записывается в виде:

Условие нормировки:

Для решения системы дифференциальных уравнений используется преобразование Лапласа, которое имеет формализованный вид:

  и обозначается как  ,

где: F(P) – изображение функции P(t); P – оператор преобразования.

Исходная система состояний энергоблока записывается в виде формализованной системы с учетом обозначений:

Начальные условия:

Применяем преобразование Лапласа:

Подставляя вместо коэффициентов  их значения, получим:

Так как работоспособным является только нулевое состояние энергоблока, то необходимо найти только  по формулам обратного преобразования Лапласа.

Решается система относительно , где D – определитель матрицы.

D =  =

Определитель  получается заменой первого столбца определителя D на столбец из значений правой части системы уравнений:

 = =

После преобразований найдём:

где: 

Подставляются известные численные данные:

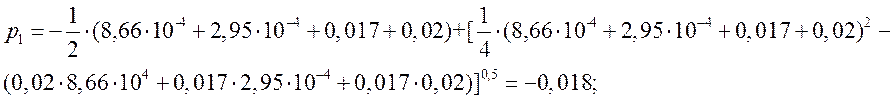
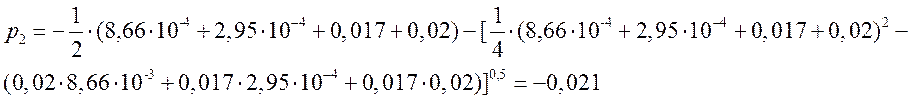
Раскладываем на простые дроби:

         Для нахождения неизвестных коэффициентов А, В, С составляется система уравнений:          

Отсюда находится:

Подставляем численные значения:

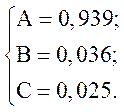
Используя обратное преобразование Лапласа для выражения с учетом , находится: .

Значит, ;

Значения вероятности безотказной работы совпадают с нестационарными значениями коэффициента готовности энергоблока .

;

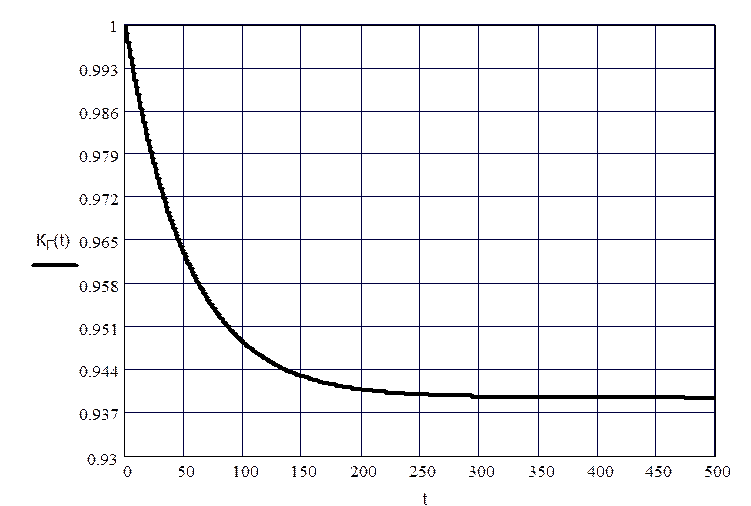
Рис. 4. Коэффициент готовности  энергоблока мощностью 100МВт.

При , а при ;

Стационарный коэффициент готовности .

Стационарный коэффициент готовности также можно найти из системы алгебраических уравнений для расчета вероятностей состояний:

Решение систем относительно P по правилу Крамера дает:

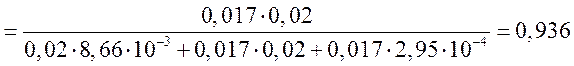
4.3. Расчет коэффициента готовности котельной в теплоэнергетической системе.

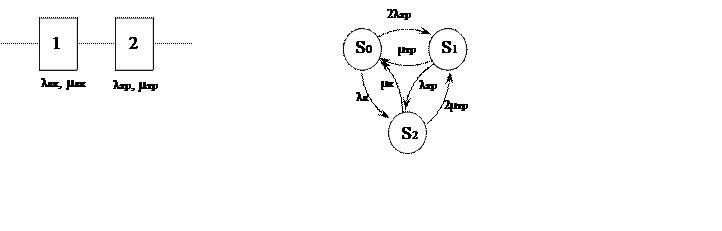
        Котельная представляется в виде структурной схемы, состоящей из трех элементов: водогрейного котла и двух магистральных теплопроводов (Рис.5а).

Достижимые состояния котельной из графа достижимых состояний (Рис.5б):

- схема теплоснабжения работоспособна (водогрейный котел и оба теплопровода находятся в работе);

- схема теплоснабжения работоспособна (в работе водогрейный котел и

один магистральный теплопровод);

 и  - состояния отказа, которые наступают при одновременном

выходе из строя обоих магистральных теплопроводов или отказе водогрейного котла.

Следует отметить, что отпуск тепла осуществляется по двум магистральным теплопроводам, каждый из которых имеет стопроцентную пропускную способность.

                        а)                                                                  б)

Рис.5. Структурная схема (а) и граф достижимых состояний котельной(б):1 – водогрейный котел; 2 – магистральные теплопроводы;

 – достижимые состояния ( ).

Система  уравнений для схемы при стационарном потоке событий  для графа состояний будет иметь вид:

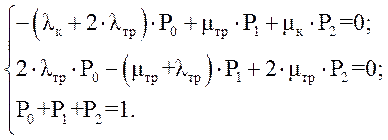
Где: условие нормировки: .

И в числовом выражении:

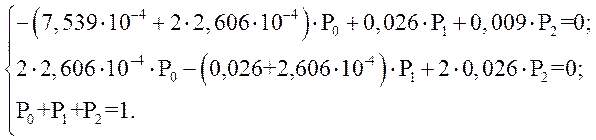
Для решения системы уравнений воспользуемся программой Mathcad и получим:

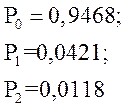
Коэффициент стационарной  готовности котельной определяем как: