6. Решение матричной игры линейно – программным способом
Графическим способом решаются не все матричные игры. Более универсальным методом решения матричных игр является линейно-программный способ. Для его применения матричная игра представляется в виде пары задач линейного программирования для игроков с условиями максимизации гарантированного выигрыша игрока А и минимизации гарантированного проигрыша игрока В.
Составим эти задачи. Пусть выигрыш игрока А, который он получит при любой стратегии игрока В. Нужно определить максимальное значение этого выигрыша.
Выигрыш игрока А
,
который он получит вне зависимости игры
игрока В, удовлетворяет условию: выигрыш
игрока А для любой стратегии игрока В
больше либо равен выигрыша
:
,
=
1, 2, … , m.
Также выполняется условие нормировки
для вероятностей стратегий игрока А:
=1.
Цель задачи
max.
Получим задачу линейного программирования,
которую назовём задачей для игрока А:
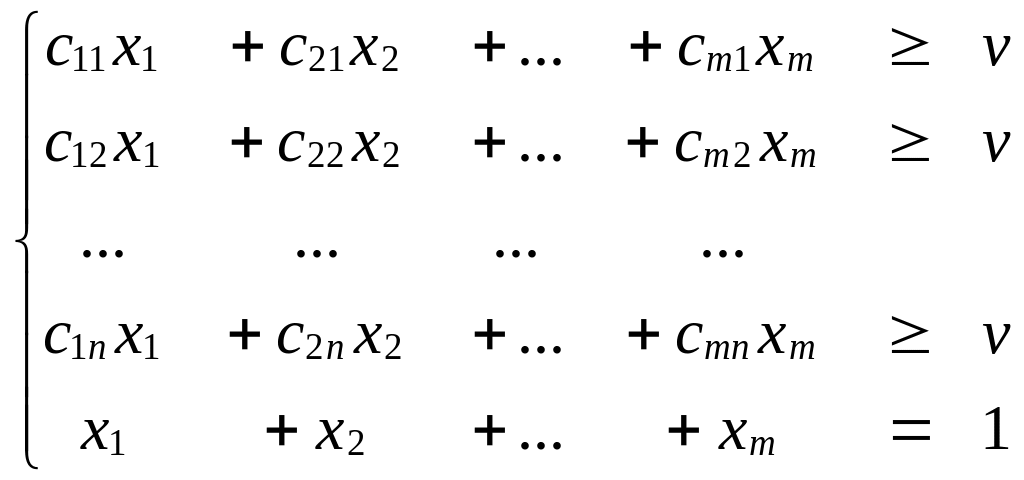(1)
Обозначим через
проигрыш игрока В, который он получит
при любой стратегии игрока А. Тогда
проигрыш игрока В для любой стратегии
игрока А больше либо равен проигрыша
:
,
=
1, 2, … , n.
Для вероятностей стратегий игрока В
также выполняется условие нормировки:
=1.
Цель задачи
min.
Это тоже задача линейного программирования,
которую назовём задачей для игрока В:
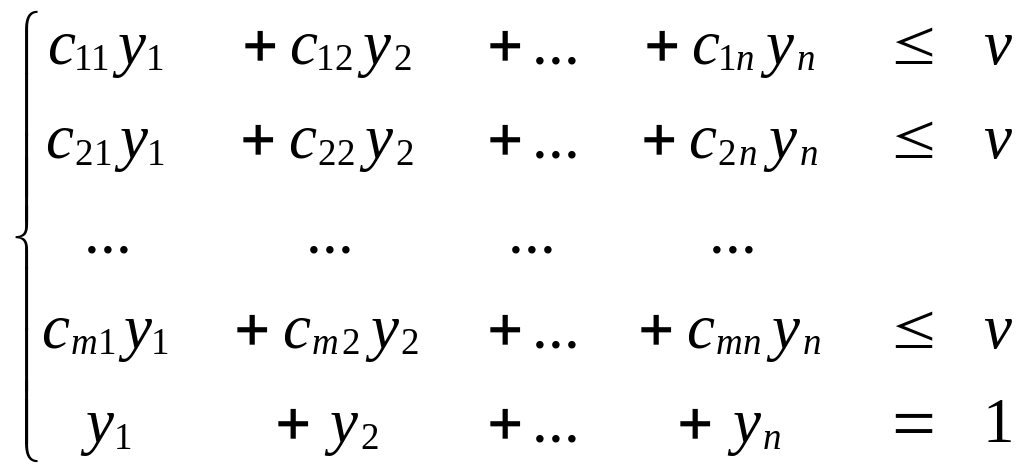(2)
Предположим, что в обеих задачах 0. Разделим все ограничения в задачах на . Получим следующие задачи.
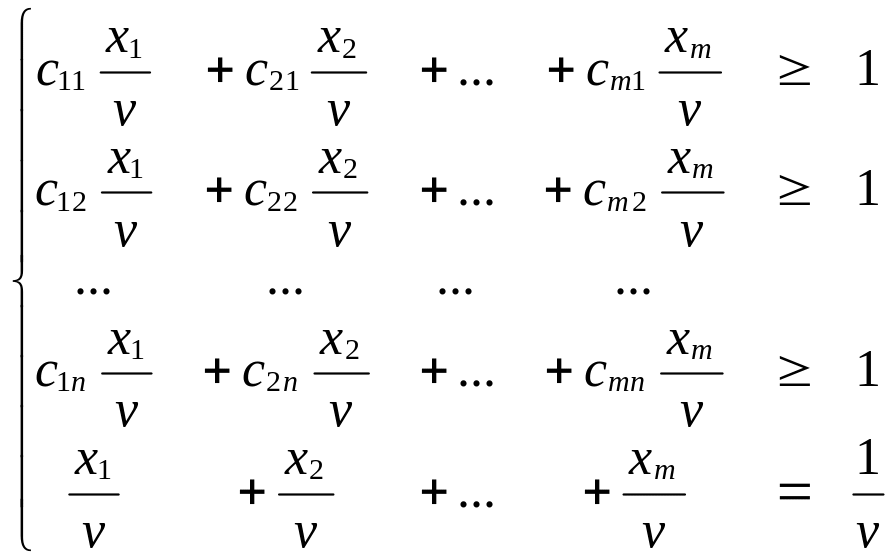(3),
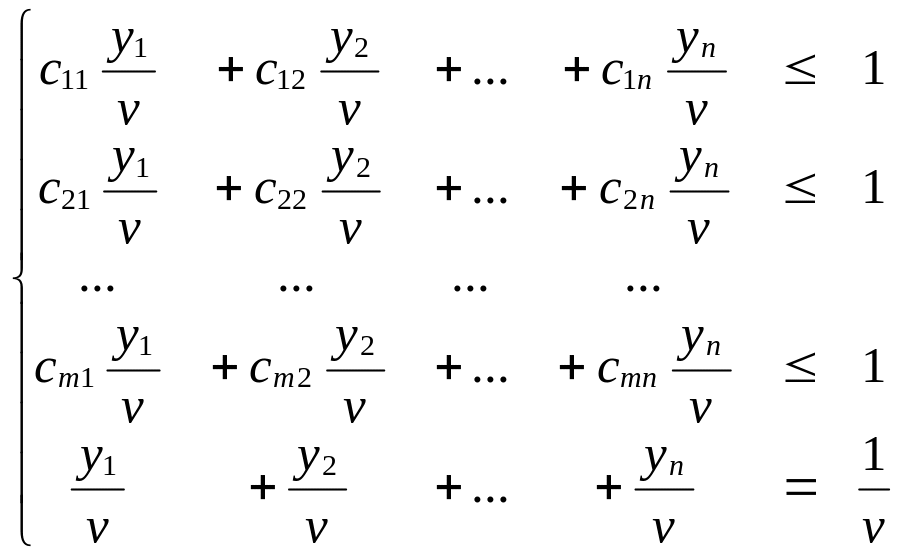(4).
Определим для обеих задач
новые переменные:
=
,
=1,
2, … , m;
=
,
=1,
2, … , n. Так
как в задачах для игроков
0,
=1,
2, … , m;
0,
=1,
2, … , n; а по
предположению
0,
то
0,
=1,
2, … , m,
0,
=1,
2, … , n.
Целевые функции в задачах определим:
=
– для задачи игрока А, и
=
– для задачи игрока В. Так как в задаче
для игрока А,
,
то
=
.
В задаче для игрока В
,
тогда
=
.
В результате получим преобразованные
задачи для игроков.
Для игрока А Для игрока В
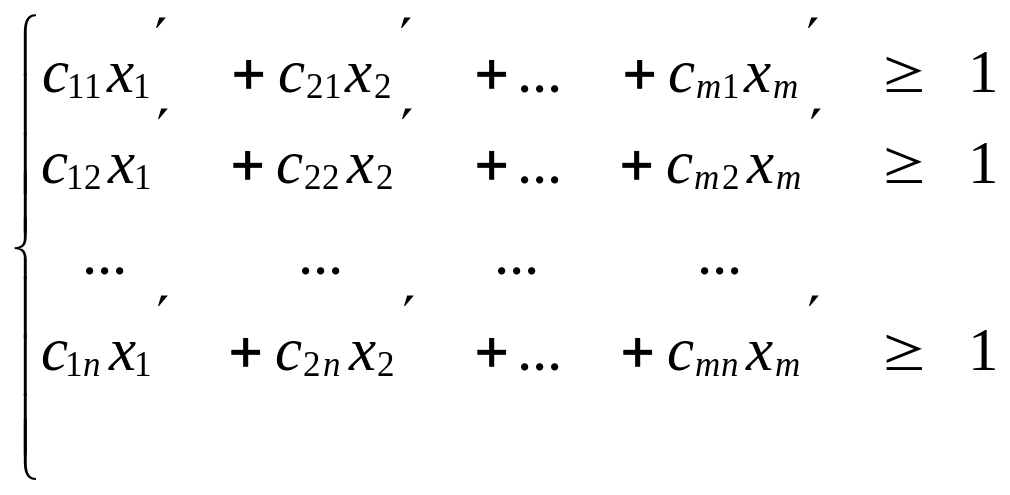(5)
(6)
Преобразованные задачи игроков являются двойственными друг к другу. При этом прямой задачей будет задача для игрока В, а двойственной – задача для игрока А. Решая одну из них, одновременно решаем и другую. Эти задачи можно решить симплекс – методом.
Переход к решению исходных задач для игроков осуществляется следующим образом.
Пусть
=
,
и
=
,
– решения пары преобразованных задач
игроков.
Переменные исходных и
преобразованных задач связаны формулами:
=
,
=1,
2, … , m;
=
,
=1,
2, … , n.
Целевые функции задач связаны с выигрышем
и проигрышем игроков
,
.
Поэтому переход к исходным задачам
осуществляется преобразованиями:
=
,
=1,
2, … , m;
=
,
=1,
2, … , n.
Целевые функции задач связаны с выигрышем
и проигрышем игроков
,
.
Тогда
=
и
=
.
Тогда формулы перехода от решения
преобразованных задач к решению исходных
задач следующие:
=
,
=1,
2, … , m;
=
,
=1,
2, … , n;
=
или
=
.
Пример 4. Для матричной игры
с платёжной матрицей
=
определить оптимальные стратегии
игроков и цену игры линейно – программным
способом.
Решение. Отметим, что в платёжной матрице все элементы строго больше нуля, поэтому цена игры в задаче будет тоже строго больше нуля. Поэтому можно использовать линейно – программный способ решения. Составим преобразованные задачи для игрока А и для игрока В.
Для игрока А Для игрока В
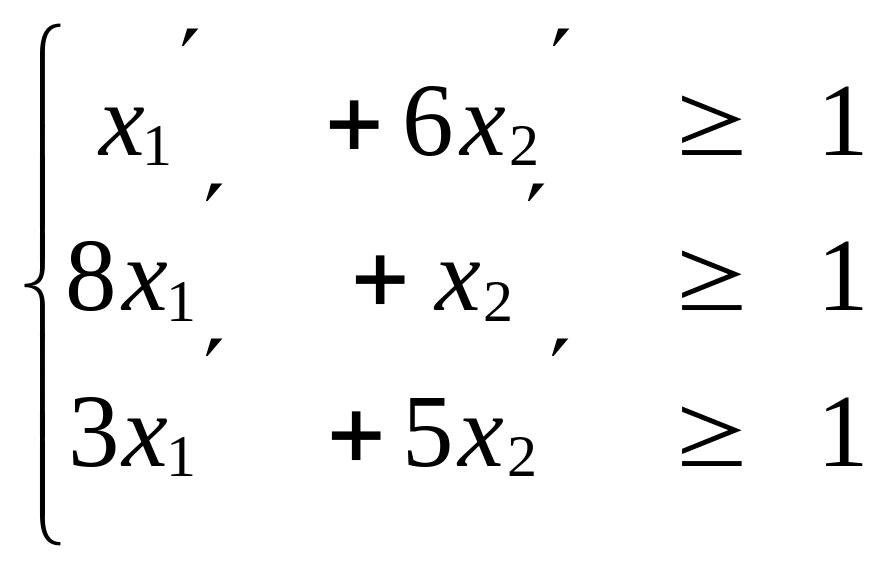(7)
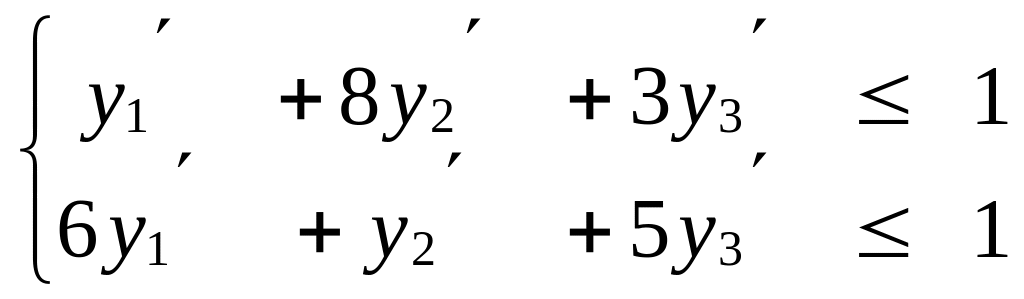(8)
Составим симплекс – таблицу для пары двойственных задач. Полагаем, что прямой задачей будет задача для игрока В. Пометим её номером ноль, полагая таблицу исходной.
0 |
|
|
|
1, |
|
1 |
8 |
3 |
1 |
|
6 |
1 |
5 |
1 |
,1 |
–1 |
–1 |
–1 |
0 |
=1
и
=1
больше либо равны нуля, то таблица
соответствует допустимому плану.
Проверяем таблицу на оптимальность. Так как в Z – строке есть строго отрицательные элементы, например
=
–1, то таблице соответствует неоптимальному
плану. 1) Так как
=
–1<0, то второй столбец выбираем
разрешающим столбцом. Элементы второго
столбца выделим серым цветом. 2) Разрешающую
строку выбираем по минимальному
симплексному отношению.
=
=
;
=
=1.
=
.
Первую строку выбираем разрешающей
строкой. Элементы разрешающей строки
выделим тоже серым цветом. 3) Разрешающим
будет элемент, расположенный на
пересечении разрешающей строки и
разрешающего столбца. Это элемент
=8.
Выделим клетку, где находится этот
элемент. 4) Проводим преобразование
таблицы с помощью исключений Жордана
– Гаусса.
1 |
|
|
|
1, |
|
1/8 |
1/8 |
3/8 |
1/8 |
|
47/8 |
–1/8 |
37/8 |
7/8 |
,1 |
–7/8 |
1/8 |
–5/8 |
1/8 |
и
местами. Остальные переменные оставляем
на своих местах. 1) Находим новое значение
разрешающего элемента
=
;
находим новые значения элементов
разрешающей строки. Значения элементов
делим на разрешающий элемент.
=
,
=
,
=
.
3) Вычисляем значения элементов
разрешающего столбца. Элементы столбца
делим на разрешающий элемент и умножаем
на минус единицу.
=
,
=
=
.
4) Пересчитываем остальные элементы по
правилу прямоугольника.
=
=
,
=
=
,
=
=
,
=
=
,
=
=
,
=
=
.
Проверяем таблицу на
оптимальность. Она не соответствует
оптимальному плану, так как
=
0.
1) Разрешающий столбец третий, так как
=
0.
2) Симплексные отношения для третьего
столбца:
=
=
1;
=
=
.
=
.
Разрешающей возьмём вторую строку. 3)
Разрешающий элемент
=
.
4) Переходим к следующей таблице.
Предварительно пересчитаем
элементы Z
– строки.
=
=
,
=
=
=
=
,
=
=
=
=
=
.
Таблица соответствует оптимальному
плану.
2 |
|
|
|
1, |
|
|
|
|
5/47 |
|
|
|
|
7/47 |
,1 |
7/47 |
5/47 |
3/47 |
12/47 |
=
=
.
=
=
=
,
=
=
=
=
.
Выписываем оптимальное
решение пары преобразованных задач.
=
,
=
,
=
,
=
.
Переходим к оптимальному
решению пары исходных задач.
=
=
;
=
=
=
=
,
=
=
=
;
=
=
=
,
=
=
=
.
Получаем оптимальные стратегии игроков
и цену игры:
=
;
=
;
=
.
Ответ: = ; = ; = .
Если в матричной игре нет гарантии строгой положительности цены, то сначала для неё составляют другую задачу, в которой все элементы платёжной матрицы строго больше нуля. Для этого находят в матрице наибольший по модулю элемент и ко всем элементам матрицы прибавляют число, равное модулю этого числа плюс единица. Тогда в полученной матрице все элементы будут строго больше нуля, а значит и цена игры будет строго больше нуля. Оптимальные стратегии полученной игры будут такие же, как в исходной игре, а цена игры увеличится на добавленное число.
Пример 5. Для матричной игры с платёжной матрицей = определить оптимальные стратегии игроков и цену игры линейно – программным способом.
Решение. В этой матричной
игре есть отрицательные элементы.
Гарантии строгой положительности цены
игры нет. Более того, мы её уже находили
графическим способом, и она была меньше
нуля. Наибольший модуль имеет отрицательное
число равное –3, их даже два. Тогда в
качестве числа, которое прибавим к
элементам матрицы возьмём
=
=3+1=4.
Мы получим платёжную матрицу
=
,
которую уже решили линейно – программным
способом. Решение матричной игры с
изменённой платёжной матрицей будет
следующим:
=
;
=
;
=
.
Переходим к решению исходной
матричной игры. Оптимальные стратегии
будут такими же:
=
;
=
,
а цена игры равна:
=
=
–4=
.
Мы получили такое же решение, как и в примере 1.
Таким образом, чтобы решить задачу линейно – программным способом, нужно проверить, все её элементы строго больше нуля или нет. Если есть отрицательные элементы, то нужно предварительно прибавить число , которое равняется наибольшему из модулей отрицательных элементов матричной игры плюс единица.