5. Решение матричной игры графическим способом.

Рассмотрим матричную игру в смешанных стратегиях, в которой у игрока А две стратегии. Платёжная матрица такой игры будет иметь вид = . Изобразим графически, как определяются выигрыши игрока А в смешанных стратегиях для одной стратегии игрока В, стратегии В₁ (рис. 1). На оси абсцисс будем откладывать точки определяющие смешанную стратегию игрока А, а именно, точке сопоставим смешанную стратегию игрока А = . Через точки =0 и =1 проведём перпендикулярно оси А₁А₁ и А₂А₂, на которых будем откладывать проигрыши игрока В при стратегиях А₁ и А₂ соответственно, если игрок В выберет стратегию В₁ (рис. 1). Эти точки обозначим В₁. Тогда на отрезке В₁В₁ будут определяться выигрыши игрока А для его смешанных стратегий = . 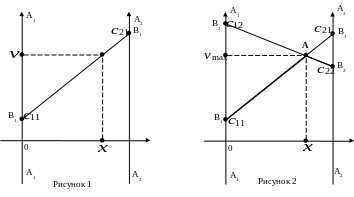Если игрок В выберет чистую стратегию В₁, в точке с координатами отрезка В₁В₁ б удет определять выигрыш игрока А для смешанной стратегии . Этот выигрыш равен: = .

Также строится и отрезок для стратегии В₂, который обозначим В₂В₂ (рис. 2). На нём будут лежать точки, определяющие выигрыши игрока для его смешанных стратеги, если игрок В выберет стратегию В₂.

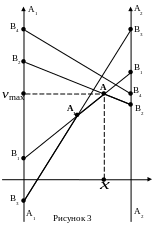Построим отрезок для второй стратегии игрока В (рис. 2). Для двух стратегий В₁ и В₂ гарантированный выигрыш игрока А составит = . Точки, определяющие гарантированные выигрыши игрока А будут лежать на ломанной, ограничивающей оба отрезка снизу. Это ломанная В₁ВВ₂ (рис. 2).

Если также отложить отрезки для всех стратегий игрока В (рис. 3), то ломанная, ограничивающая эти отрезки снизу будет определять гарантированные выигрыши игрока А для смешанных стратегий в матричной игре с платёжной матрицей = . Выигрыш на этой ломанной определяется значениями = . На рисунке 3 рассмотрен пример для четырёх стратегий. На нём ломаная, ограничивающая отрезки В₁В₁, В₂В₂, В₃В₃ и В₄В₄ снизу, будет ломанная В₃А₁АВ₂.

Игрок А выберет ту смешанную стратегию, при которой гарантированный выигрыш будет наибольшим. Поэтому, на ломанной он выберет точку с наибольшим значением выигрыша, это точка . На рисунке 3 она изображена как точка пересечения отрезков В₁В₁ и В₂В₂. По отрезкам В₁В₁ и В₂В₂ определяются проигрыши игрока В, если он выбирает стратегии В₁ и В₂. Игроку В выгодно использовать эти стратегии, так как он будет получать меньший проигрыш по сравнению с другими своими стратегиями. Стратегии В₁ и В₂ будем называть активными для игрока В, а остальные стратегии игрока В, которые не проходят через точку А, пассивными. Игрок А может предположить, что игроку В выгодно придерживаться активных стратегий В₁ и В₂.

Найдём оптимальную стратегию игрока А. Составляем систему уравнений для активных стратегий игрока В, предполагая, что выигрыш игрока А по активным стратегиям игрока В равняется наибольшему гарантированному выигрышу игрока А, цене игры . В систему уравнений добавляется условие нормировки, определяющее, что сумма вероятностей игрока А для его смешанной стратегии равняется единицы.

Для нашего случая получаем систему уравнений: 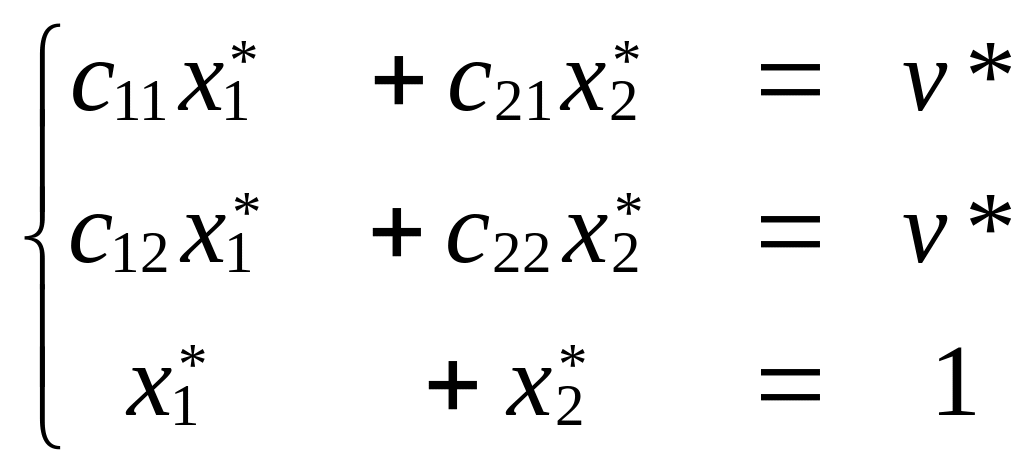. Эта задача называется задачей для игрока А.

Если точка А будет точкой пересечения трёх и более отрезков, то все стратегий, отрезки которых пересекают точку А будут активными, для всех стратегий записывается условие, что для оптимальной стратегии игрока А его выигрыш равен .

Д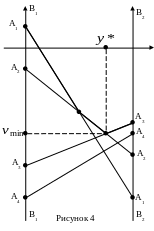 ля игрока В ставится задача, исходя из условий, что его проигрыш для активных стратегий равняется . Для пассивных стратегий игрока В вероятности выбора равна нулю. Поэтому сумма вероятностей выбора активных стратегий равна единице. Для матричной игры, которую мы рассматриваем, задача игрока В будет иметь вид: 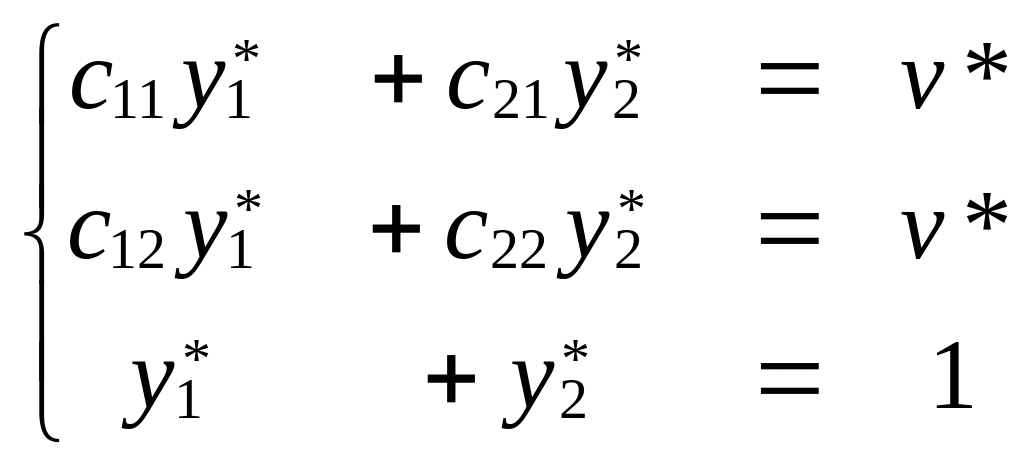. Значение в обеих задачах должно быть одинаковым. Это является и контрольным вычислением для правильности решения матричной игры.

Когда оптимальной стратегией является чистая стратегия игрока А, то условие проигрыша игрока В равного составляется только для этой чистой стратегии игрока А, которая оказалась оптимальной.

Рассмотрим матричную игру, в которой, игрок В имеет две стратегии. В этой задаче на оси абсцисс точки определяют смешенные стратегии игрока В (рис. 4), а именно, стратегии игрока В = . На осях В₁В₁ и В₂В₂ (рис. 4) откладываются выигрыши игрока А для его чистых стратегий, если игрок В выбирается свои чистые стратегии В₁ и В₂ соответственной. Отрезки, соединяющие выигрыши игрока А для одной стратегии игрока А, будут определять проигрыши игрока В для его смешанных стратегий, если игрок А выберет соответствующую чистую стратегию.

Ломанная, определяющая гарантированные проигрыши игрока В, будет ограничивать отрезки, определяющие для игрока А его выигрыши при чистых стратегиях, сверху. Точка ломанной , имеющая самый наименьший гарантированный проигрыш, определяет оптимальную стратегию игрока В. Также определяются активные стратегии игрока А. Отрезки этих стратегий пересекают точку В.

В этом случае задача игрока В определяется из условий, что его гарантированный проигрыш для активных стратегий игрока А равен = и сумма вероятностей выбора обеих стратегий игроком В равна единице.

Задача для игрока А определяется из условий, что для его активных стратегий выигрыш при выборе игроком В своих чистых стратегий равняется , а сумма вероятностей для активных стратегий игрока А равна единице.

В случае, когда оптимальной смешанной стратегией игрока В является его чистая стратегия. Тогда для игрока А записывается условие, что для этой чистой стратегии выигрыш игрока А для его активных стратегий равняется .

Пример 1. Для матричной игры с платёжной матрицей = определить оптимальные стратегии игроков и цену игры графическим способом.

Р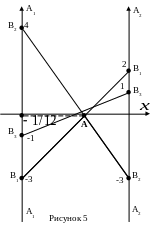 ешение. Построим график для определения проигрышей игрока В для различных смешанных стратегий игрока А (рис. 5). На оси А₁А₁ отметим проигрыши игрока В для его стратегий, если игрок А выберет стратегию А₁. Отмечаем точку В₁ с координатой равной –3, точку В₂ с координатой 4 и точку В₃ с координатой –1. На оси А₂А₂ отметим проигрыши игрока В, если игрок А выберет стратегию А₂: В₁ (2), В₂ (–3), В₃ (1). Соединяем соответствующие точки на разных осях, получаем отрезки В₁В₁, В₂В₂ и В₃В₃. Определяем ломанную, ограничивающую отрезки снизу. Это ломанная В₁АВ₂. На ломанной выбираем точку с наибольшим выигрышем игрока А. Это точка А. Она является точкой пересечения отрезков В₁В₁ и В₂В₂. Для игрока В стратегии В₁ и В₂ активные, а стратегия В₃ – пассивная. Вероятность =0.

Составляем задачу для игрока В. Записываем условия для каждой стратегии игрока А, что, математическое ожидание проигрыша игрока В для его активных стратегий равняется цене игры. А также условие нормировки для активных стратегий.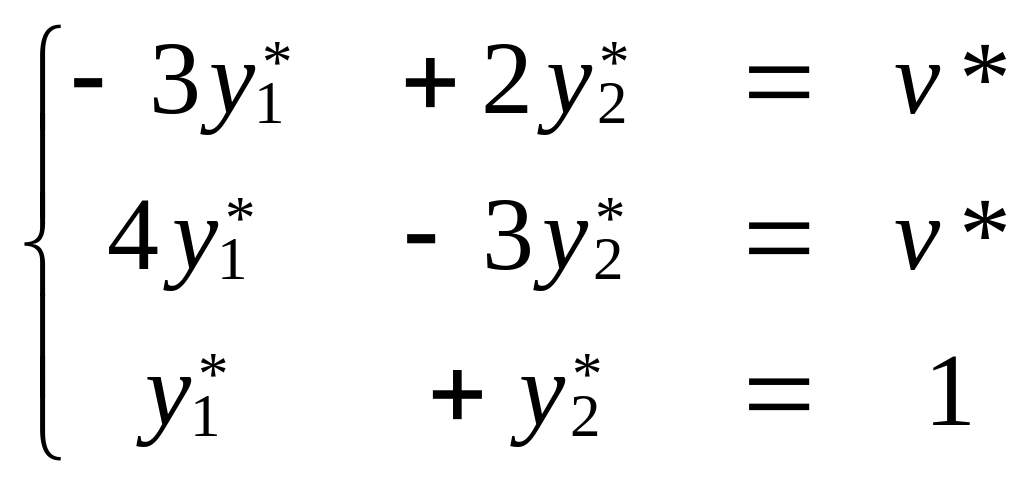 . Решим эту систему уравнений. Из первых двух уравнений = = . Тогда или . Выражение для подставляем в третье уравнение: . Находим значение : = = . Находим значение : = = . Подставляем значения и в первое уравнение: = = = . Второе уравнение используем для проверки решения системы:

= = = . Система уравнений решена верно.

Составляем задачу для игрока А. Записываем условия равенства математического ожидания выигрыша игрока А для каждой активной стратегии игрока В и условие нормировки для всех стратегий.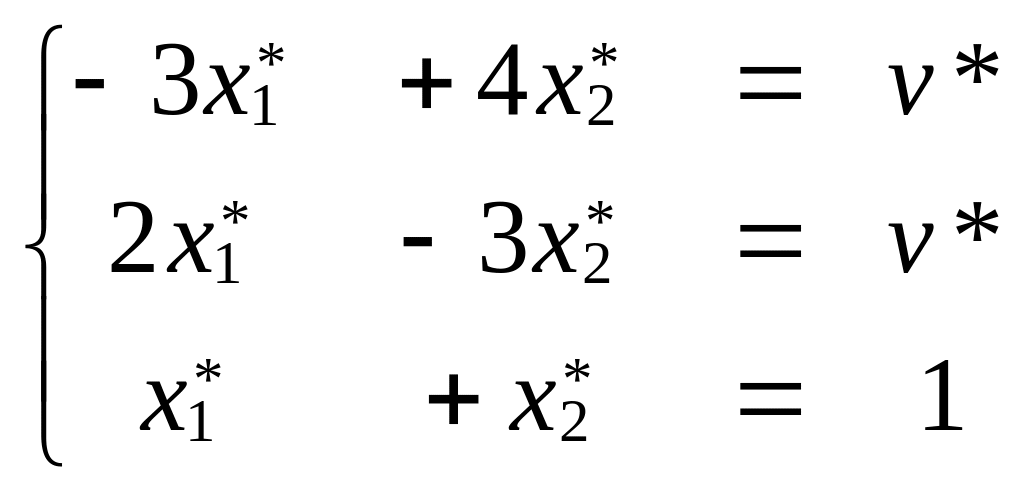 . Из первых двух уравнений: = . Тогда или . Из третьего уравнения: . = = . = = . Подставляем в первое уравнение: = = = . Во втором уравнении = = = = . Задача для игрока В решена верно. Ответ: = ; = ; = .

Пример 2. Для матричной игры с платёжной матрицей =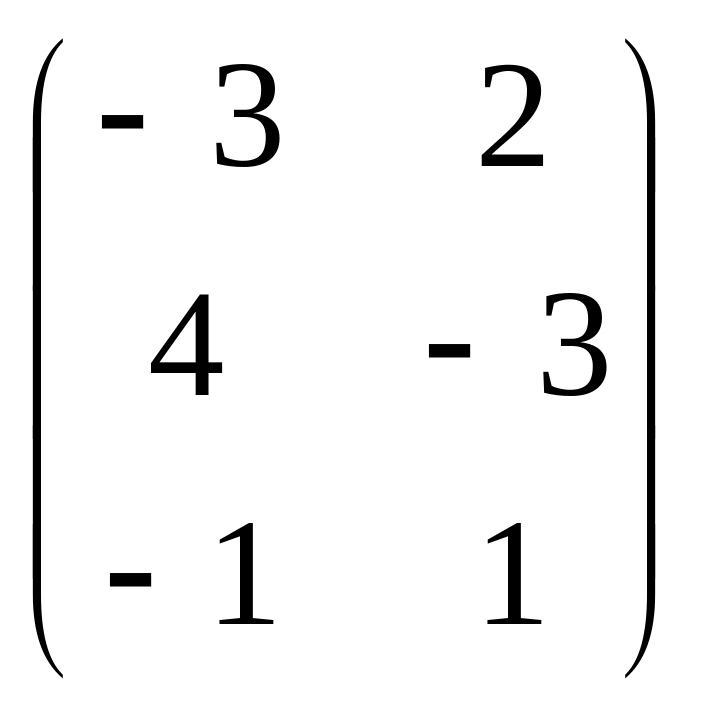 определить оптимальные стратегии игроков и цену игры графическим способом.

Р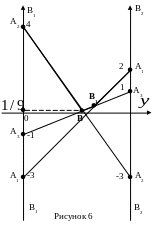 ешение. В этой задаче построим график для определения выигрышей игрока А (рис. 6). На осях В₁В₁ и В₂В₂ отметим выигрыши игрока А, если игрок А выберет стратегии А₁ и А₂ соответственно. На оси В₁В₁ точки: А₁ (–3), А₂ (4), А₃ (–1); на оси В₂В₂ точки: А₁ (2), А₂ (–3), А₃ (1). Строим отрезки А₁А₁, А₂А₂ и А₃А₃. Строим ломанную, ограничивающую отрезки сверху. Это ломанная А₂ ВВ₁А₁. На ломанной точка с наименьшим проигрышем игрока В будет точка В. Это точка пересечения отрезков А₂А₂ и А₃А₃. Стратегии А₂ и А₃ активные, а стратегия А₁ – пассивная. Вероятность =0.

Составим задачу для игрока А. 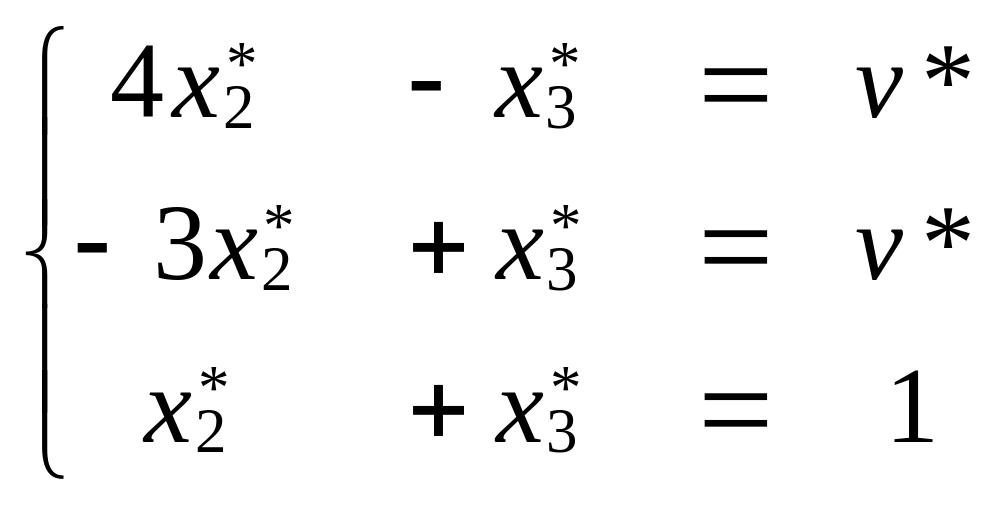. Из первых двух уравнений: = . Тогда или . Из третьего уравнения: . = = . = = . Находим цену игры: = = = = . Проверка: = = = . Составим задачу для игрока В. 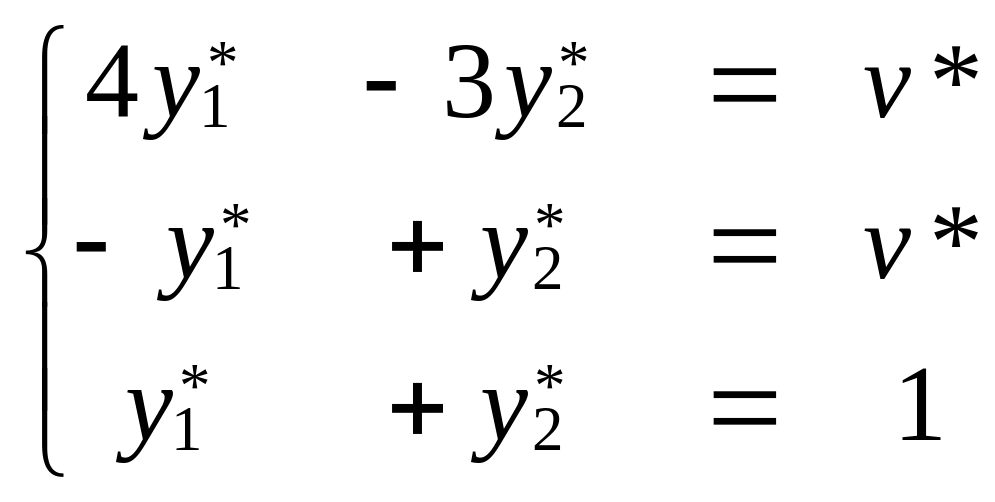. = = . Тогда или . Выражение для подставляем в третье уравнение: . Находим значение : = = . Находим : = = . Подставляем значения и в первое уравнение: = = = . Ответ: = ; = ; = .

Пример 3. Для матричной игры с платёжной матрицей =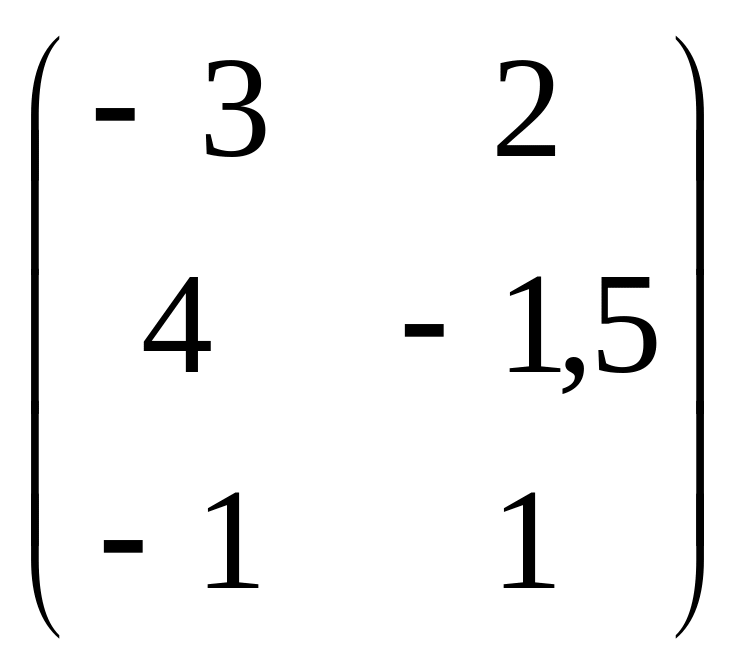 определить оптимальные стратегии игроков и цену игры графическим способом.

Решение. Строим график для определения выигрышей игрока А (рис. 7). На осях В₁В₁ и В₂В₂ отмечаем выигрыши игрока А. На оси В₁В₁ точки: А₁ (–3), А₂ (4), А₃ (–1); на оси В₂В₂ точки: А₁ (2),

А₂ (–1,5), А₃ (1). Строим отрезки А₁А₁, А₂А₂ и А₃А₃. Ограничивающую отрезки сверху ломанной А₂ ВА₁. На ломанной выбираем точку В. Это точка пересечения отрезков А₁А₁, А₂А₂ и А₃А₃. Все три стратегии А₁, А₂ и А₃ активные. В задаче для игрока А записываем условие равенства математического ожидания выигрыша цене игры всех активных стратегий игрока А для каждой стратеги игрока В.

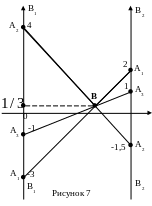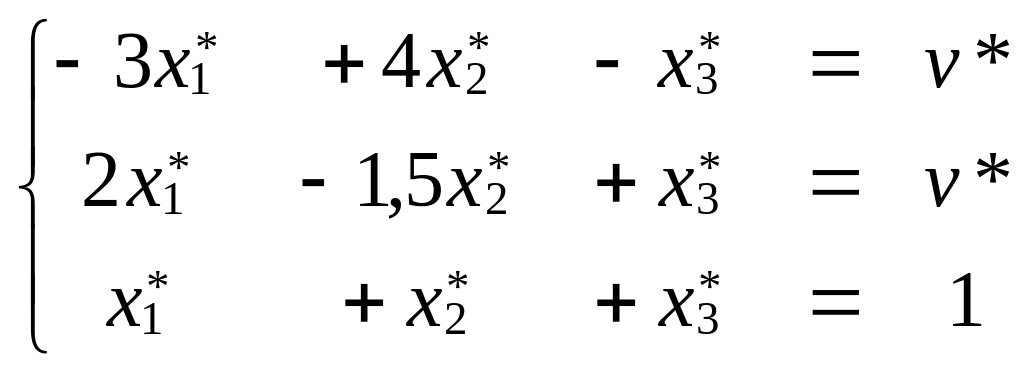З адача для игрока А. . Из первых двух уравнений: = = . Тогда или . Из третьего уравнения: . = = . = = . Находим цену игры: = = = . Проверка: = = = = . Переменные , и больше равны нуля и меньше равны единице. Положим = . Тогда для выполняются двойные неравенства: , , . Найдём решения второго и третьего двойных неравенств.

; .

. Для переменной выполняются ограничения: .

Решением задачи для игрока А будут стратегии = , где ; = .

Составим задачу для игрока В из условия равенства математического ожидания проигрыша игрока В цене игры для активных стратегий игрока А. 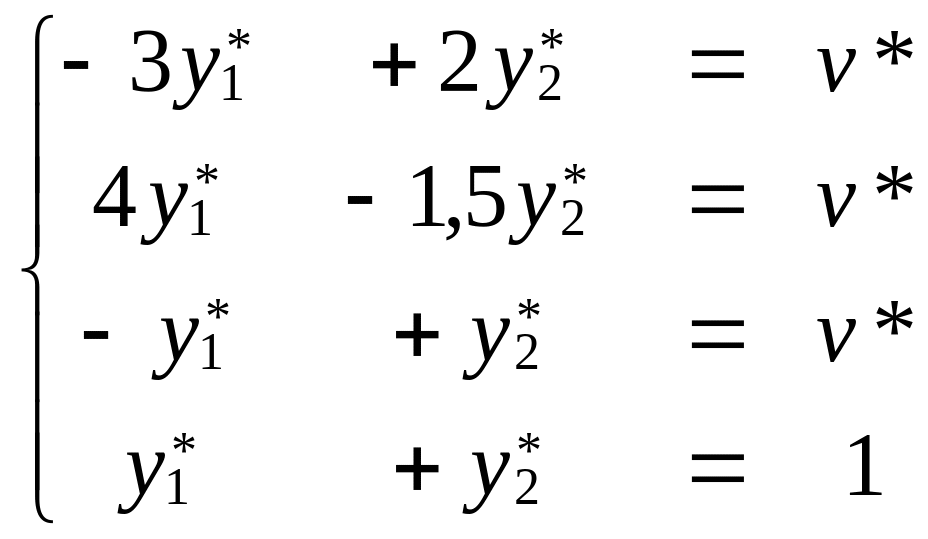. = = . Тогда или . Выражение для подставляем в третье уравнение: . Находим значение : = . Находим : = = . Подставляем значения и в первое уравнение: = = . Сделаем проверку в третьем уравнении: = . Решение для задачи игрока В: = ; = = .

Ответ: = , где ; = ; = .